74. 搜索二维矩阵

🟠   🔖  数组 二分查找 矩阵  🔗 力扣 LeetCode

题目

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix orfalse otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3

Output: true

Example 2:

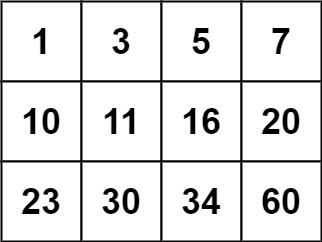
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13

Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

题目大意

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

解题思路

思路一：从右上角遍历

这道题说 matrix 从上到下递增，从左到右递增，显然左上角是最小元素，右下角是最大元素。我们如果想高效在 matrix 中搜索一个元素，肯定需要从某个角开始，比如说从左上角开始，然后每次只能向右或向下移动，不要走回头路。

如果真从左上角开始的话，就会发现无论向右还是向下走，元素大小都会增加，那么到底向右还是向下？不确定，那只好用类似 动态规划算法 的思路穷举了。

但实际上不用这么麻烦，我们不要从左上角开始，而是从右上角开始，规定只能向左或向下移动。

你注意，如果向左移动，元素在减小，如果向下移动，元素在增大，这样的话我们就可以根据当前位置的元素和 target 的相对大小来判断应该往哪移动，不断接近从而找到 target 的位置。

复杂度分析

• 时间复杂度：O(m + n)，因为从右上角向下、向左遍历，最坏情况下需要判断 m+n 次；
• 空间复杂度：O(1)，只使用了常数的额外空间。

---

思路二：二分查找

可以将这个问题看作在一个排序的一维数组中查找目标值的二分查找问题。虽然矩阵是二维的，但由于矩阵每行和每列都严格递增，可以将二维矩阵“展开”为一维数组来进行处理。

1. 二维矩阵转为一维数组的思想：
   • 假设矩阵有 m 行 n 列，矩阵的第 i 行第 j 列的元素，可以映射到一维数组中的下标 index = i * n + j。
   • 反过来，一维数组的索引 index 对应到二维矩阵中的行列位置则为：row = index / n | 0, col = index % n。
2. 二分查找：
   • 可以把整个矩阵看作是一个长度为 m * n 的排序数组，然后直接对这个数组进行二分查找。
   • 计算中间位置 mid，将其映射回二维矩阵中的 row 和 col。
   • 如果中间值等于目标值，返回 true。
   • 如果中间值小于目标值，说明目标值在右半部分，移动左边界。
   • 如果中间值大于目标值，说明目标值在左半部分，移动右边界。
   • 当左边界超过右边界时，说明没有找到目标值，返回 false。

复杂度分析

• 时间复杂度：O(log(m * n))，这是一个标准的二分查找的时间复杂度，其中 m 是行数，n 是列数。
• 空间复杂度：O(1)，只使用了常数的额外空间。

代码

从右上角遍历

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
	const h = matrix.length;
	const w = matrix[0].length;
	// 从右上角开始遍历矩阵
	let i = 0;
	let j = w - 1;
	while (i < h && j >= 0) {
		if (matrix[i][j] == target) return true; // 找到目标值
		if (matrix[i][j] < target) {
			i++; // 向下移动
		} else {
			j--; // 向左移动
		}
	}
	return false;
};

二分查找

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
	const m = matrix.length,
		n = matrix[0].length;
	let left = 0,
		right = m * n - 1;
	while (left <= right) {
		const mid = ((left + right) / 2) | 0;
		const i = (mid / n) | 0, // 映射回二维矩阵中的行
			j = mid % n; // 映射回二维矩阵中的列
		if (matrix[i][j] == target) {
			return true; // 找到目标值
		} else if (matrix[i][j] > target) {
			right = mid - 1; // 移动左边界
		} else if (matrix[i][j] < target) {
			left = mid + 1; // 移动右边界
		}
	}

	return false;
};

相关题目

题号	标题	题解	标签	难度	力扣
240	搜索二维矩阵 II	[✓]	数组 二分查找 分治 1+	🟠	🀄️ 🔗
2468	根据限制分割消息		字符串 二分查找	🔴	🀄️ 🔗