146. LRU 缓存

🟠   🔖  设计 哈希表 链表 双向链表  🔗 力扣 LeetCode

题目

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.

Implement the LRUCache class:

• LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
• int get(int key) Return the value of the key if the key exists, otherwise return -1.
• void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.

Follow up:Could you do get and put in O(1) time complexity?

Example 1:

Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]

Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1);    // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2);    // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1);    // return -1 (not found)
lRUCache.get(3);    // return 3
lRUCache.get(4);    // return 4

Constraints:

• 1 <= capacity <= 3000
• 0 <= key <= 10^4
• 0 <= value <= 10^5
• At most 2 * 105 calls will be made to get and put.

题目大意

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
• 函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

解题思路

LRU 是 Least Recently Used 的缩写，即最近最少使用，是一种常用的缓存淘汰算法，选择最久未使用的页面予以淘汰。

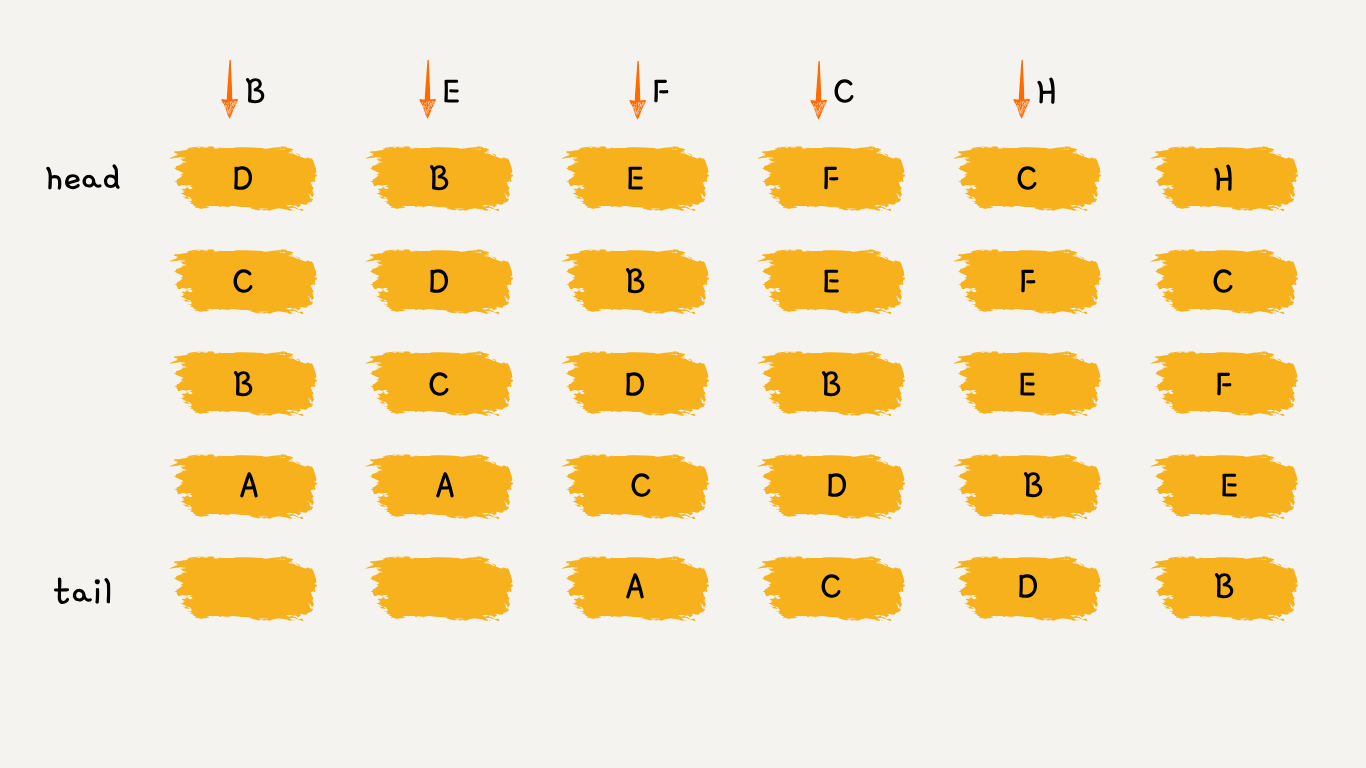
可以维护一个有序单链表，越靠近链表尾部的节点是越早之前访问的。如上图所示：

• 要插入 B 的时候，发现缓存中有 B ，这时需要把 B 放到链首，因为它被使用了；
• 要插入 E 的时候，缓存中没有 E，直接把 E 插入链首；
• 要插入 F 的时候，缓存中没有 F，容量已满，需要淘汰掉 A ，因为 A 最久未被使用；
• 要插入 C 的时候，发现缓存中有 C ，这时需要把 C 放到链首；
• 要插入 H 的时候，缓存中没有 H，容量已满，需要淘汰掉 D ，因为 D 最久未被使用；

可以发现，LRU 更新和插入新节点都发生在链首，删除数据都发生在链尾。

LRUCache 类有两个方法：

• get 当有一个新的数据被访问时：
  • 如果此数据之前已经被缓存在链表中了，遍历得到这个数据对应的节点，并将其从原来的位置删除，然后再插入到链表的头部，返回数据的值；
  • 如果此数据没有在缓存链表中，则返回 -1；
• put 往链表里新增数据时：
  • 如果此数据之前已经被缓存在链表中了，更新此数据的值，并将其从原来的位置删除，再插入到链表的头部；
  • 如果此数据没有在缓存链表中，又分为两种情况：
    • 如果此时缓存未满，则将此节点直接插入到链表的头部；
    • 如果此时缓存已满，则链表尾节点删除，将新的数据节点插入链表的头部。

这样就用链表实现了一个 LRU 缓存，如果使用单向链表实现，则缓存访问的时间复杂度为 O(n)，因为不管缓存有没有满，都需要遍历一遍链表。

可以继续优化这个实现思路，比如使用双向链表，并引入 哈希表（Hash table） 来记录每个数据的位置，将缓存访问的时间复杂度降到 O(1)。

代码

class Node {
	// @param {number} key
	// @param {number} value
	constructor(key, value) {
		this.key = key;
		this.value = value;
		this.next = null;
		this.prev = null;
	}
}

class LRUCache {
	// @param {number} capacity
	constructor(capacity) {
		this.cap = capacity;
		this.cache = new Map();
		this.head = new Node(0, 0);
		this.tail = new Node(0, 0);
		this.head.next = this.tail;
		this.tail.prev = this.head;
	}

	// @param {number} key
	// @return {number}
	get(key) {
		if (this.cache.has(key)) {
			this.remove(this.cache.get(key));
			this.insert(this.cache.get(key));
			return this.cache.get(key).value;
		}
		return -1;
	}

	// @param {Node} node
	remove(node) {
		const prev = node.prev;
		const next = node.next;
		prev.next = next;
		next.prev = prev;
	}

	// @param {Node} node
	insert(node) {
		const next = this.head.next;
		this.head.next = node;
		next.prev = node;
		node.prev = this.head;
		node.next = next;
	}

	// @param {number} key
	// @param {number} value
	// @return {void}
	put(key, value) {
		if (this.cache.has(key)) {
			this.remove(this.cache.get(key));
		}
		this.cache.set(key, new Node(key, value));
		this.insert(this.cache.get(key));
		if (this.cache.size > this.cap) {
			const old = this.tail.prev;
			this.remove(old);
			this.cache.delete(old.key);
		}
	}
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */

相关题目

题号	标题	题解	标签	难度	力扣
460	LFU 缓存	[✓]	设计 哈希表 链表 1+	🔴	🀄️ 🔗
588	设计内存文件系统 🔒		设计 字典树 哈希表 2+	🔴	🀄️ 🔗
604	迭代压缩字符串 🔒		设计 数组 字符串 1+	🟢	🀄️ 🔗
1756	设计最近使用（MRU）队列 🔒		栈 设计 树状数组 3+	🟠	🀄️ 🔗