109. 有序链表转换二叉搜索树

🟠   🔖  树 二叉搜索树 链表 分治 二叉树  🔗 力扣 LeetCode

题目

Given the head of a singly linked list where elements are sorted in ascending order , convert it to a height-balanced binary search tree.

Example 1:

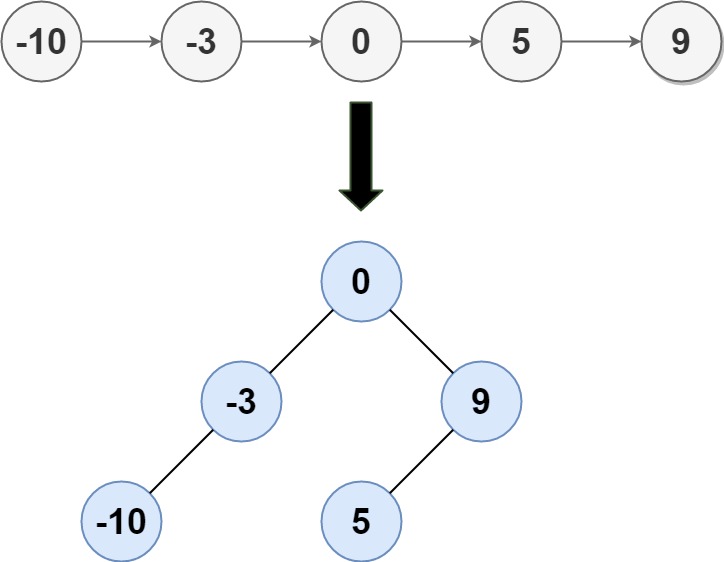
Input: head = [-10,-3,0,5,9]

Output: [0,-3,9,-10,null,5]

Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []

Output: []

Constraints:

• The number of nodes in head is in the range [0, 2 * 10^4].
• -10^5 <= Node.val <= 10^5

题目大意

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

解题思路

可以通过递归的方式实现，使用快慢指针找到链表的中间节点，并以中间节点为根构建左右子树。

1. 找到链表的中间节点： 为了构建平衡二叉搜索树，我们需要找到链表的中间节点作为根节点。可以通过快慢指针的方式，一个指针每次走两步，另一个指针每次走一步，直到快指针到达链表末尾，慢指针即为中间节点。在这个过程中，用一个 prev 指针指向中间节点的前一个节点，方便从中间切断链表。

2. 以中间节点为根构建左右子树： 将找到的中间节点作为当前子树的根节点，然后递归地构建左子树和右子树。对于左子树，递归处理链表的前半部分；对于右子树，递归处理链表的后半部分。

3. 递归终止条件： 在递归过程中，当链表为空或只有一个节点时，直接返回对应的树节点。这是递归的终止条件。

4. 返回根节点： 最终返回根节点作为整棵平衡二叉搜索树的根。

代码

/**
 * @param {ListNode} head
 * @return {TreeNode}
 */
var sortedListToBST = function (head) {
	if (!head) return null;

	// 使用快慢指针找到链表中间节点
	let slow = head;
	let fast = head;
	let prev = null;
	while (fast && fast.next) {
		prev = slow;
		slow = slow.next;
		fast = fast.next.next;
	}

	// 中间节点作为根节点
	let root = new TreeNode(slow.val);

	// 递归构建左右子树
	if (prev) {
		prev.next = null; // 切断链表
		root.left = sortedListToBST(head);
	}
	root.right = sortedListToBST(slow.next);

	return root;
};

相关题目

题号	标题	题解	标签	难度	力扣
108	将有序数组转换为二叉搜索树	[✓]	树 二叉搜索树 数组 2+	🟢	🀄️ 🔗
2196	根据描述创建二叉树	[✓]	树 数组 哈希表 1+	🟠	🀄️ 🔗