36. 二叉搜索树与双向链表

🟠   🔖  栈 树 深度优先搜索 二叉搜索树 链表 二叉树 双向链表  🔗 力扣

题目

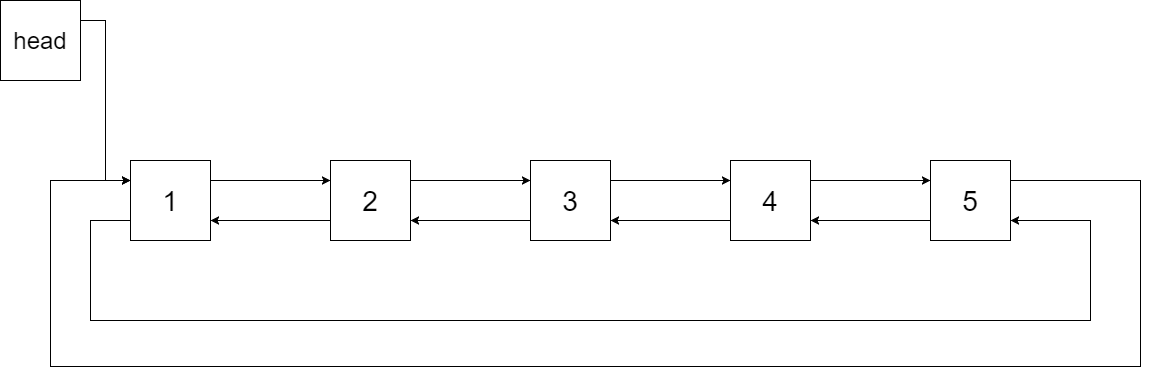
将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以 就地 完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

示例 1：

输入：root = [4,2,5,1,3]

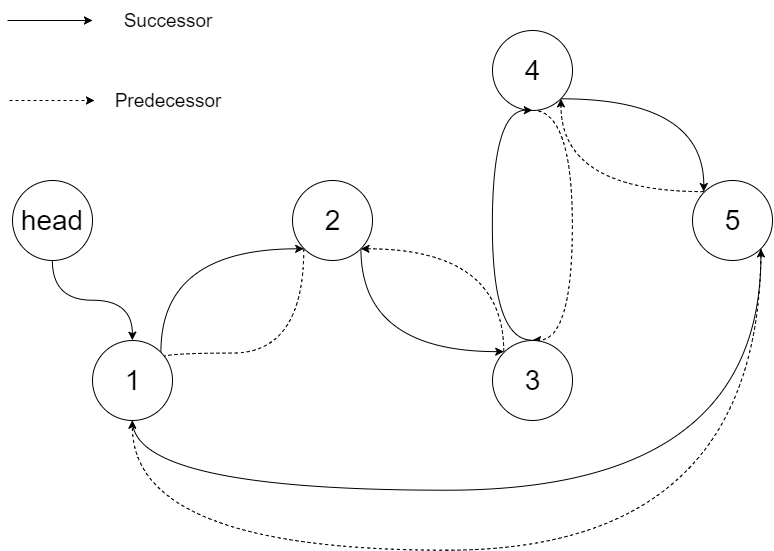
输出：[1,2,3,4,5]

解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

示例 2：

输入：root = [2,1,3]

输出：[1,2,3]

示例 3：

输入：root = []

输出：[]

解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]

输出：[1]

提示：

• -1000 <= Node.val <= 1000
• Node.left.val < Node.val < Node.right.val
• Node.val 的所有值都是独一无二的
• 0 <= Number of Nodes <= 2000

提示：

注意

本题与 LeetCode 第 426 题 相同。

解题思路

二叉搜索树的中序遍历结果是有序的，因此要将一个二叉搜索树就地转化为一个已排序的双向循环链表，可以采用中序遍历的方式，将节点的左右指针分别指向前驱和后继节点。最后，调整头尾节点的前驱和后继指针，形成循环链表。

1. 定义两个指针 head 和 tail，它们分别表示双向链表的头部和尾部。
2. 定义一个中序遍历的函数 traverse，其中对每个节点进行如下处理：
   • 如果 head 为空，将当前节点赋值给 head。
   • 如果 tail 不为空，将 tail 的右指针指向当前节点，将当前节点的左指针指向 tail。
   • 更新 tail 为当前节点。
3. 在 traverse 完成中序遍历后，将 head 和 tail 进行连接，形成双向循环链表。
   • 将 head 的左指针指向 tail。
   • 将 tail 的右指针指向 head。

这样，我们就完成了将 BST 转化为已排序的双向循环链表。最后，返回 head 作为循环链表的头节点。

复杂度分析

• 时间复杂度: O(n)，其中 n 是二叉搜索树的节点数量。因为我们需要访问每个节点一次，完成中序遍历。
• 空间复杂度: O(h)，其中 h 是二叉搜索树的高度，表示递归调用栈的深度。

代码

/**
 * @param {Node} root
 * @return {Node}
 */
var treeToDoublyList = function (root) {
	if (!root) return null;
	let head = null;
	let tail = null;

	const traverse = (root) => {
		if (!root) return null;
		traverse(root.left);

		// 处理当前节点
		if (!head) {
			head = root;
		}
		if (tail) {
			tail.right = root;
			root.left = tail;
		}
		tail = root;

		traverse(root.right);
	};

	// 开始中序遍历
	traverse(root);

	// 将头尾相连形成循环链表
	head.left = tail;
	tail.right = head;
	return head;
};