4. 二维数组中的查找

🟠   🔖  数组 二分查找 分治 矩阵  🔗 力扣

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

输入: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5

输出: true

示例 2：

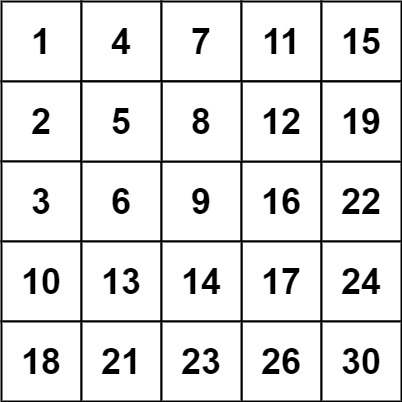
输入: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20

输出: false

说明：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -10^9 <= matrix[i][j] <= 10^9
• 每行的所有元素从左到右升序排列。
• 每列的所有元素从上到下升序排列。
• -10^9 <= target <= 10^9

注意

本题与 LeetCode 第 240 题 相同。

解题思路

这道题说 matrix 从上到下递增，从左到右递增，显然左上角是最小元素，右下角是最大元素。我们如果想高效在 matrix 中搜索一个元素，肯定需要从某个角开始，比如说从左上角开始，然后每次只能向右或向下移动，不要走回头路。

如果真从左上角开始的话，就会发现无论向右还是向下走，元素大小都会增加，那么到底向右还是向下？不确定，那只好用类似 动态规划算法 的思路穷举了。

但实际上不用这么麻烦，我们不要从左上角开始，而是从右上角开始，规定只能向左或向下移动。

你注意，如果向左移动，元素在减小，如果向下移动，元素在增大，这样的话我们就可以根据当前位置的元素和 target 的相对大小来判断应该往哪移动，不断接近从而找到 target 的位置。

代码

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
	const h = matrix.length;
	const w = matrix[0].length;
	let i = 0;
	let j = w - 1;
	while (i < h && j >= 0) {
		if (matrix[i][j] == target) return true;
		if (matrix[i][j] > target) {
			j--;
		} else {
			i++;
		}
	}
	return false;
};