33. 二叉搜索树的后序遍历序列

🟠   🔖  栈 树 二叉搜索树 递归 数组 二叉树 单调栈  🔗 力扣

题目

请实现一个函数来判断整数数组 postorder 是否为二叉搜索树的后序遍历结果。

示例 1：

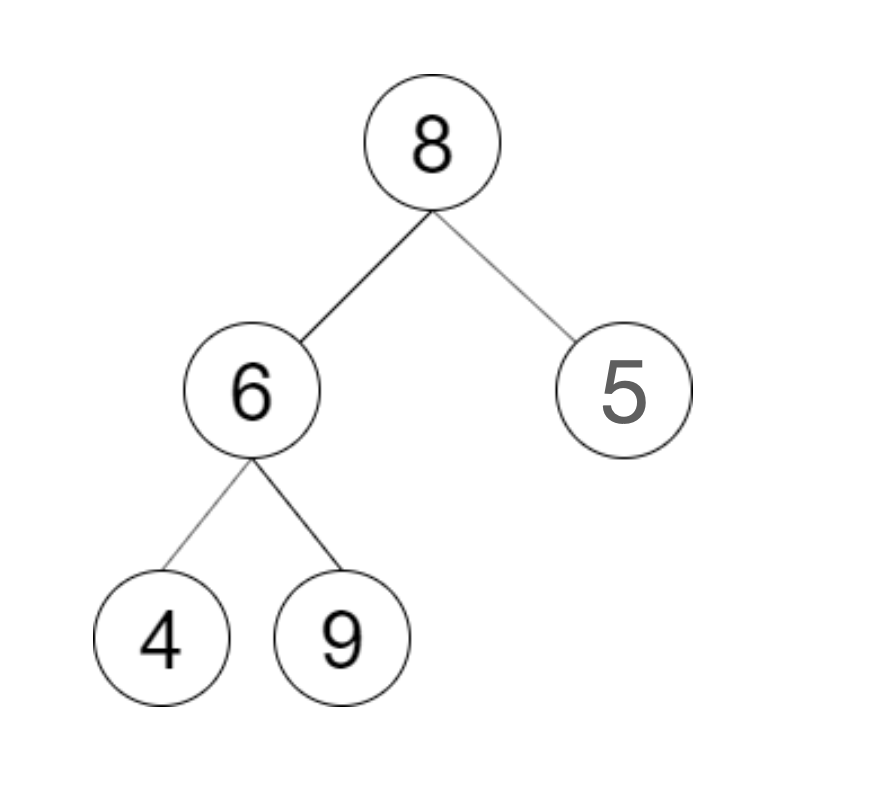
输入: postorder = [4,9,6,5,8]

输出: false

解释：从上图可以看出这不是一颗二叉搜索树

示例 2：

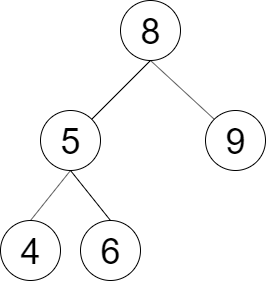
输入: postorder = [4,6,5,9,8]

输出: true

解释：可构建的二叉搜索树如上图

提示：

• 数组长度 <= 1000
• postorder 中无重复数字

解题思路

• 后序遍历结果的特点是：左边一部分是左子树，右边一部分是右子树，最后一个元素是根节点。
• BST 的特点是：左子树元素都小于根节点，右子树元素都大于根节点。

结合上述规律，就可以得到本题的解题思路：

1. 先找到根节点元素
2. 根据根节点元素找到左子树元素，递归检查左子树是否是 BST
3. 根据根节点元素找到右子树元素，递归检查右子树是否是 BST

代码

/**
 * @param {number[]} postorder
 * @return {boolean}
 */
var verifyTreeOrder = function (postorder) {
	const len = postorder.length;
	if (len == 0) return true;

	// 根节点的值是后序遍历结果的最后一个元素
	let root = postorder[len - 1];

	// postorder[0..left) 是左子树，应该都小于 root
	let left = 0;
	while (left < len - 1 && postorder[left] < root) {
		left++;
	}

	// postorder[left..len - 1) 是右子树，应该都大于 root
	let right = left;
	while (right < len - 1 && postorder[right] > root) {
		right++;
	}

	if (right !== len - 1) {
		return false;
	}

	// 递归检查左子树 [0..left) 和右子树 [left..len - 1) 也符合 BST 的性质
	return (
		verifyTreeOrder(postorder.slice(0, left)) &&
		verifyTreeOrder(postorder.slice(left, len - 1))
	);
};