3.4 回溯算法

回溯的定义

定义

回溯（Backtracking） 又称为试探法，是一种通过不断地尝试，搜索问题的解的算法。它是一种深度优先搜索的过程，通常通过递归实现。回溯算法主要用于解决组合问题、排列问题和搜索问题，其核心思想是穷尽所有可能性，找到满足条件的解。

通过尝试不同的可能性，逐步构建问题的解，当达到某个条件或无法继续扩展时，就进行回退，尝试其他的可能性。

回溯算法和我们常说的 DFS 算法非常类似，本质上就是一种暴力穷举算法。回溯算法和 DFS 算法的细微差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」。

回溯的原理

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。站在回溯树的一个节点上，只需要思考 3 个问题：

路径：也就是已经做出的选择。
选择列表：也就是你当前可以做的选择。
结束条件：也就是到达决策树底层，无法再做选择的条件。

代码方面，回溯算法的框架：

let result = [];
let track = []; // 路径
const backtrack = (选择列表) => {
	if (满足结束条件) {
		result.add(track);
		return;
	}

	for (选择 in 选择列表) {
		// 做选择
		track.push(选择);
		// 递归调用
		backtrack(选择列表);
		// 撤销选择
		track.pop();
	}
};

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。

下面我们就通过LeetCode 第 46 题全排列open in new window 来了解什么叫做选择和撤销选择，以及这个框架的底层原理。

题目大意

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。nums 中的所有整数 互不相同。

高中的时候做过排列组合的数学题， n 个不重复的数，全排列共有 n! 个。那么是怎么穷举全排列的呢？比方说给三个数 [1,2,3]，一般是这样：

先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……

其实这就是回溯算法，可以直接画出如下这棵回溯树：

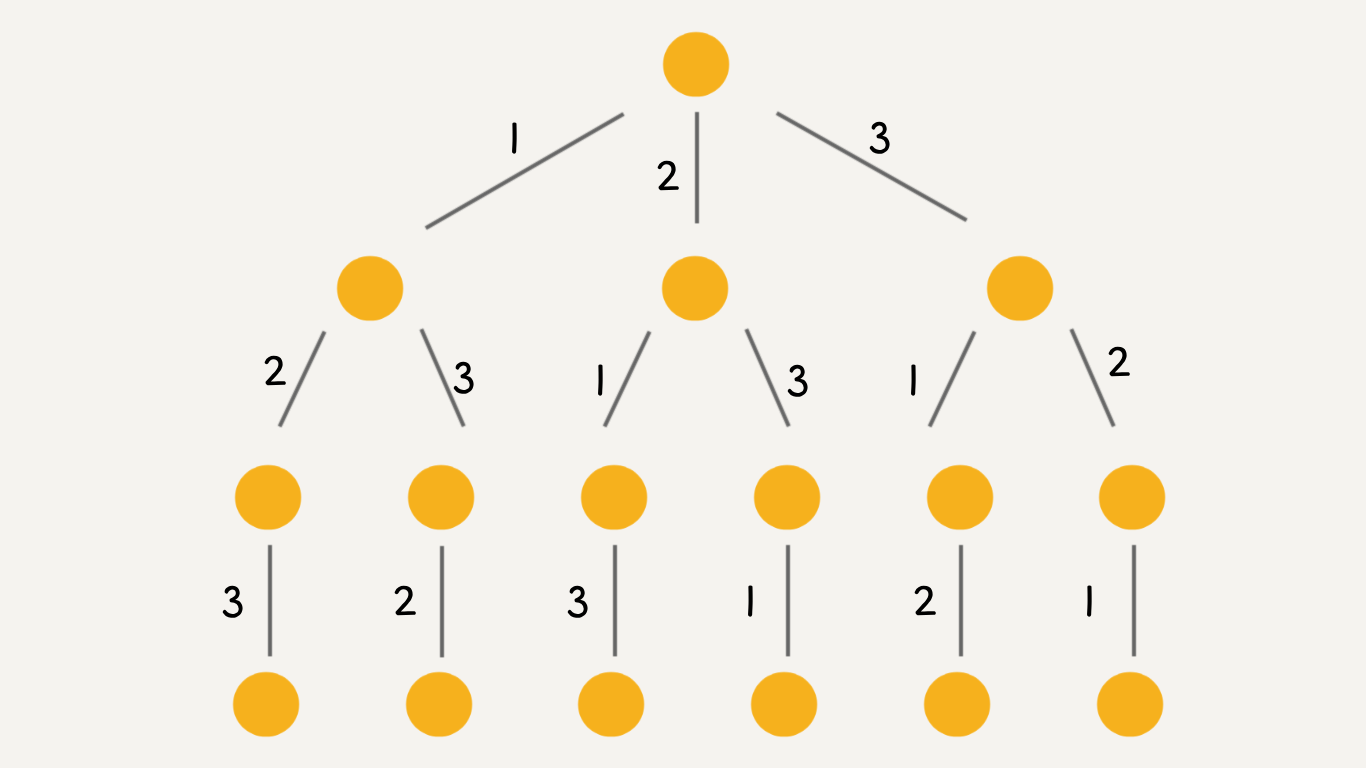
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。 不妨把这棵树称为回溯算法的「决策树」，因为你在每个节点上其实都在做决策。 比如说站在下图的红色节点上，就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在身后，这个选择之前做过了，而全排列是不允许重复使用数字的。

现在可以解答上面的几个名词：[2] 就是「路径」，记录已经做过的选择；[1,3] 就是「选择列表」，表示当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列。

全排列的代码如下：

var permute = function (nums) {
	const n = nums.length;
	let res = [];
	let used = new Array(n).fill(false);

	const backtrack = (track) => {
		if (track.length == n) {
			res.push([...track]);
			return;
		}

		for (let i = 0; i < n; i++) {
			if (used[i]) {
				continue;
			}

			// 做选择
			track.push(nums[i]);
			used[i] = true;

			// 递归
			backtrack(track);

			// 撤销选择，回溯
			track.pop();
			used[i] = false;
		}
	};

	backtrack([]);
	return res;
};

这里稍微做了些变通，没有显式记录「选择列表」，而是通过 used 数组排除已经存在 track 中的元素，从而推导出当前的选择列表。

至此，我们就通过全排列问题详解了回溯算法的底层原理。

回溯的框架套路

虽然排列、组合、子集系列问题是高中就学过的，但如果想编写算法解决它们，还是非常考验计算机思维的，下面就讲讲编程解决这几个问题的核心思路，以后再有什么变体，也能手到擒来，以不变应万变。

无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：

变体一：元素无重不可复选
- 即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的情况。
- 以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。
变体二：元素可重不可复选
- 即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。
- 以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
变体三：元素无重可复选
- 即 nums 中的元素都是唯一的，每个元素可以被使用若干次。
- 以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。

当然，也可以说有第四种变体，即元素可重可复选。但既然元素可复选，那又何必存在重复元素呢？元素去重之后就等同于形式三，所以这种情况不用考虑。

上面用组合问题举的例子，但排列、组合、子集问题都可以有这三种基本形式，所以共有 9 种变化。

元素无重不可复选 - 子集

相关题目

📌 78. 子集 - LeetCodeopen in new window

💻 题目大意

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

💡 解题思路

比如输入 nums = [1,2,3]，算法应该返回如下子集：[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]，过程如下：

首先，生成元素个数为 0 的子集，即空集 []，为了方便表示，称之为 S_0;
然后，在 S_0 的基础上生成元素个数为 1 的所有子集: [1], [2], [3]，称为 S_1;
接着，可以在 S_1 的基础上推导出 S_2，即元素个数为 2 的所有子集：[1, 2], [1, 3], [2, 3]。
- 因为集合中的元素不用考虑顺序，[1,2,3] 中 2 后面只有 3，如果添加了前面的 1，那么 [2,1] 会和之前已经生成的子集 [1,2] 重复。
- 换句话说，通过保证元素之间的相对顺序不变来防止出现重复的子集。
接着，我们可以通过 S_2 推出 S_3，实际上 S_3 中只有一个集合 [1,2,3]，它是通过 [1,2] 推出的;

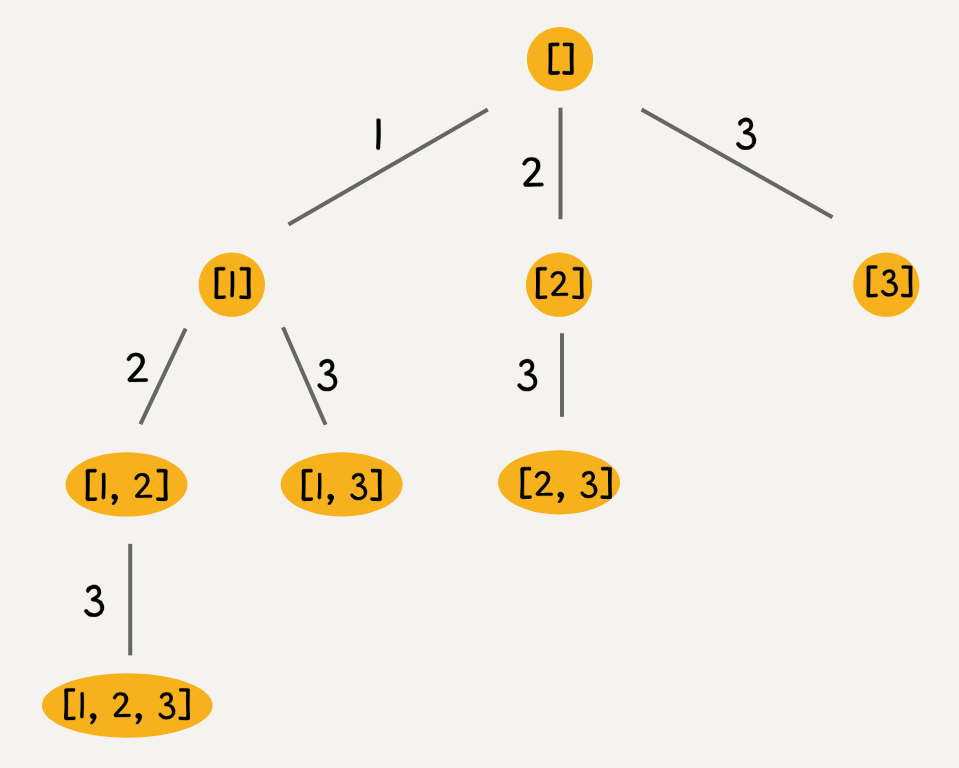
所以如果想计算所有子集，只要遍历这棵多叉树，把所有节点的值收集起来就行了。代码如下：

💎 代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
	// 用于存储结果
	const res = [];
	// 用于记录回溯路径
	const track = [];

	const backtrack = (start) => {
		// 前序遍历位置，每个节点的值都是一个子集
		res.push([...track]);

		// 回溯算法标准框架
		for (let i = start; i < nums.length; i++) {
			// 做选择
			track.push(nums[i]);
			// 回溯遍历下一层节点
			backtrack(i + 1);
			// 撤销选择
			track.pop();
		}
	};

	backtrack(0);
	return res;
};

使用 start 参数控制树枝的生长避免产生重复的子集，用 track 记录根节点到每个节点的路径的值，同时在前序位置把每个节点的路径值收集起来，完成回溯树的遍历就收集了所有子集。

backtrack 函数开头看似没有 base case，会不会进入无限递归？其实不会的，当 start == nums.length 时，叶子节点的值会被装入 res，但 for 循环不会执行，也就结束了递归。

#### 📌 [78. 子集 - LeetCode](https://leetcode.com/problems/subsets/)

#### 💻 **题目大意**

给你一个整数数组 `nums` ，数组中的元素 **互不相同** 。返回该数组所有可能的子集（幂集）。

解集 **不能** 包含重复的子集。你可以按 **任意顺序** 返回解集。

#### 💡 **解题思路**

比如输入 `nums = [1,2,3]`，算法应该返回如下子集：`[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]`，过程如下：

- 首先，生成元素个数为 `0` 的子集，即空集 `[]`，为了方便表示，称之为 `S_0`;
- 然后，在 `S_0` 的基础上生成元素个数为 `1` 的所有子集: `[1], [2], [3]`，称为 `S_1`;
- 接着，可以在 `S_1` 的基础上推导出 `S_2`，即元素个数为 `2` 的所有子集：`[1, 2], [1, 3], [2, 3]`。
  - 因为集合中的元素不用考虑顺序，`[1,2,3]` 中 `2` 后面只有 `3`，如果添加了前面的 `1`，那么 `[2,1]` 会和之前已经生成的子集 `[1,2]` 重复。
  - 换句话说，通过保证元素之间的相对顺序不变来防止出现重复的子集。
- 接着，我们可以通过 `S_2` 推出 `S_3`，实际上 `S_3` 中只有一个集合 `[1,2,3]`，它是通过 `[1,2]` 推出的;

![](../image/3-4-3.png)

所以如果想计算所有子集，只要遍历这棵多叉树，把所有节点的值收集起来就行了。代码如下：

#### 💎 **代码**

```javascript
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
	// 用于存储结果
	const res = [];
	// 用于记录回溯路径
	const track = [];

	const backtrack = (start) => {
		// 前序遍历位置，每个节点的值都是一个子集
		res.push([...track]);

		// 回溯算法标准框架
		for (let i = start; i < nums.length; i++) {
			// 做选择
			track.push(nums[i]);
			// 回溯遍历下一层节点
			backtrack(i + 1);
			// 撤销选择
			track.pop();
		}
	};

	backtrack(0);
	return res;
};
```

使用 `start` 参数控制树枝的生长避免产生重复的子集，用 `track` 记录根节点到每个节点的路径的值，同时在前序位置把每个节点的路径值收集起来，完成回溯树的遍历就收集了所有子集。

`backtrack` 函数开头看似没有 base case，会不会进入无限递归？其实不会的，当 `start == nums.length` 时，叶子节点的值会被装入 `res`，但 `for` 循环不会执行，也就结束了递归。

元素无重不可复选 - 组合

相关题目

📌 77. 组合 - LeetCodeopen in new window

💻 题目大意

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

💡 解题思路

还是以 nums = [1,2,3] 为例（ n = 3, k = 2 ），刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合：[ [1,2],[1,3],[2,3] ]。

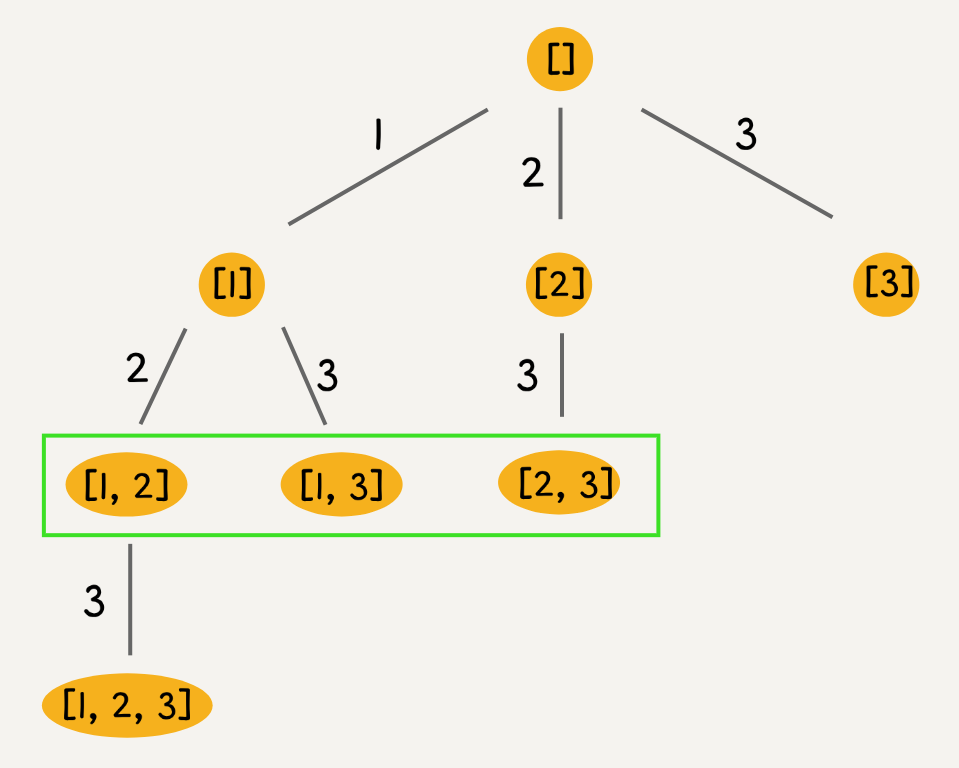
反映到代码上，只需要稍改 base case，控制算法仅收集第 k 层节点的值即可。

💎 代码

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function (n, k) {
	let res = [];
	let track = [];
	const backtrack = (start) => {
		// 仅收集第 k 层节点
		if (track.length == k) {
			res.push([...track]);
			return;
		}
		for (let i = start; i <= n; i++) {
			track.push(i);
			backtrack(i + 1);
			track.pop();
		}
	};
	backtrack(1);
	return res;
};

#### 📌 [77. 组合 - LeetCode](https://leetcode.com/problems/combinations/)

#### 💻 **题目大意**

给定两个整数 `n` 和 `k`，返回范围 `[1, n]` 中所有可能的 `k` 个数的组合。

你可以按 **任何顺序** 返回答案。

#### 💡 **解题思路**

还是以 `nums = [1,2,3]` 为例（ `n = 3, k = 2` ），刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 `2` 层（根节点视为第 `0` 层）的节点收集起来，就是大小为 `2` 的所有组合：`[ [1,2],[1,3],[2,3] ]`。

![](../image/3-4-4.png)

反映到代码上，只需要稍改 base case，控制算法仅收集第 `k` 层节点的值即可。

#### 💎 **代码**

```javascript
/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function (n, k) {
	let res = [];
	let track = [];
	const backtrack = (start) => {
		// 仅收集第 k 层节点
		if (track.length == k) {
			res.push([...track]);
			return;
		}
		for (let i = start; i <= n; i++) {
			track.push(i);
			backtrack(i + 1);
			track.pop();
		}
	};
	backtrack(1);
	return res;
};
```

元素无重不可复选 - 排列

相关题目

📌 46. 全排列 - LeetCodeopen in new window

💻 题目大意

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。nums 中的所有整数 互不相同。

💡 解题思路

比如输入 nums = [1,2,3]，函数的返回值应该是：

[
    [1,2,3],[1,3,2],
    [2,1,3],[2,3,1],
    [3,1,2],[3,2,1]
]

刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1..] 中的元素，通过固定元素的相对位置保证不出现重复的子集。

但排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套不行了，需要额外使用 used 数组来标记哪些元素还可以被选择。标准全排列可以抽象成如下这棵多叉树：

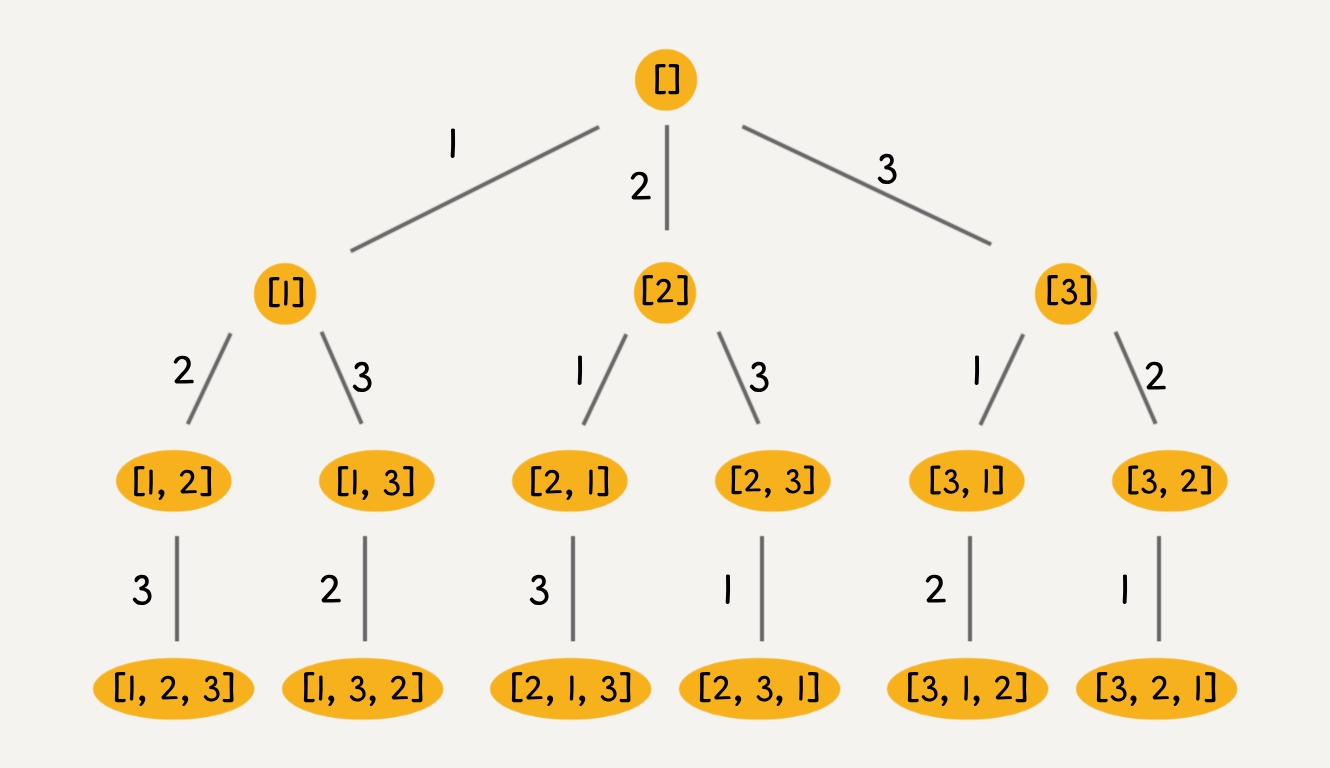
我们用 used 数组标记已经在路径上的元素避免重复选择，然后收集所有叶子节点上的值，就是所有全排列的结果。

💎 代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
	const n = nums.length;
	let res = [];
	let track = [];
	let used = new Array(n).fill(false);

	const backtrack = () => {
		if (track.length == n) {
			res.push([...track]);
			return;
		}

		for (let i = 0; i < n; i++) {
			if (used[i]) {
				continue;
			}
			// 做选择
			track.push(nums[i]);
			used[i] = true;

			// 递归
			backtrack();

			// 撤销选择，回溯
			track.pop();
			used[i] = false;
		}
	};

	backtrack();
	return res;
};

如果题目不让你算全排列，而是让你算元素个数为 k 的排列，怎么算？也很简单，改下 backtrack 函数的 base case，仅收集第 k 层的节点值即可。

const backtrack = () => {
	if (track.length == k) {
		res.push([...track]);
		return;
	}
	// ...
};

#### 📌 [46. 全排列 - LeetCode](https://leetcode.com/problems/permutations/)

#### 💻 **题目大意**

给定一个不含重复数字的数组 `nums` ，返回其 **所有可能的全排列** 。你可以 **按任意顺序** 返回答案。`nums` 中的所有整数 **互不相同**。

#### 💡 **解题思路**

比如输入 `nums = [1,2,3]`，函数的返回值应该是：

```
[
    [1,2,3],[1,3,2],
    [2,1,3],[2,3,1],
    [3,1,2],[3,2,1]
]
```

刚才讲的组合/子集问题使用 `start` 变量保证元素 `nums[start]` 之后只会出现 `nums[start+1..]` 中的元素，通过固定元素的相对位置保证不出现重复的子集。

但排列问题本身就是让你穷举元素的位置，`nums[i]` 之后也可以出现 `nums[i]` 左边的元素，所以之前的那一套不行了，需要额外使用 `used` 数组来标记哪些元素还可以被选择。标准全排列可以抽象成如下这棵多叉树：

![](../image/3-4-5.png)

我们用 used 数组标记已经在路径上的元素避免重复选择，然后收集所有叶子节点上的值，就是所有全排列的结果。

#### 💎 **代码**

```javascript
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
	const n = nums.length;
	let res = [];
	let track = [];
	let used = new Array(n).fill(false);

	const backtrack = () => {
		if (track.length == n) {
			res.push([...track]);
			return;
		}

		for (let i = 0; i < n; i++) {
			if (used[i]) {
				continue;
			}
			// 做选择
			track.push(nums[i]);
			used[i] = true;

			// 递归
			backtrack();

			// 撤销选择，回溯
			track.pop();
			used[i] = false;
		}
	};

	backtrack();
	return res;
};
```

如果题目不让你算全排列，而是让你算元素个数为 k 的排列，怎么算？也很简单，改下 `backtrack` 函数的 base case，仅收集第 `k` 层的节点值即可。

```javascript
const backtrack = () => {
	if (track.length == k) {
		res.push([...track]);
		return;
	}
	// ...
};
```

元素可重不可复选 - 子集

相关题目

📌 90. 子集 II - LeetCodeopen in new window

💻 题目大意

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

💡 解题思路

比如输入 nums = [1,2,2]，函数的返回值应该是：[ [],[1],[2],[1,2],[2,2],[1,2,2] ]

就以 nums = [1,2,2] 为例，为了区别两个 2 是不同元素，后面我们写作 nums = [1,2,2']。

按照之前的思路画出子集的树形结构，显然，两条值相同的相邻树枝会产生重复：

[
    [],
    [1],[2],[2'],
    [1,2],[1,2'],[2,2'],
    [1,2,2']
]

可以看到，[2] 与 [2']、[1,2] 与 [1,2'] 这两个结果出现了重复，所以需要进行剪枝，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：

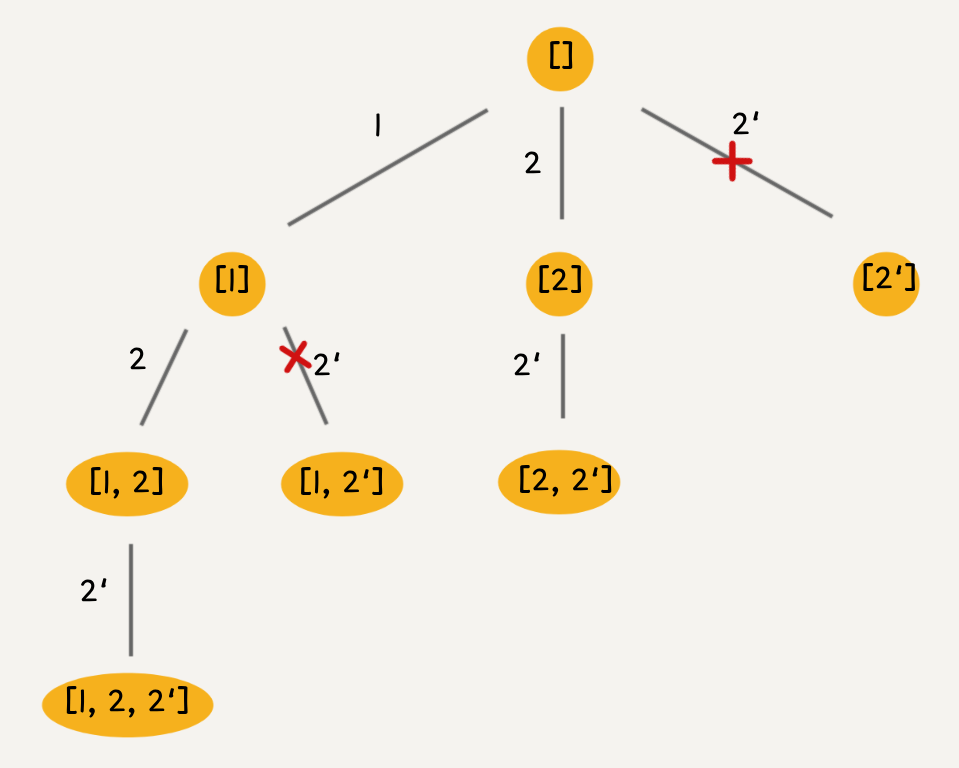
体现在代码上，需要先进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过。

代码和之前标准的子集问题的代码几乎相同，就是添加了排序和剪枝的逻辑。

💎 代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsetsWithDup = function (nums) {
	let res = [];
	let track = [];

	// 排序，以便在后续的步骤中去重
	nums.sort((a, b) => a - b);

	const backtrack = (start) => {
		res.push([...track]);

		for (let i = start; i < nums.length; i++) {
			// 出现了重复元素，跳过
			if (i > start && nums[i] == nums[i - 1]) {
				continue;
			}
			track.push(nums[i]);
			backtrack(i + 1);
			track.pop();
		}
	};

	backtrack(0);
	return res;
};

#### 📌 [90. 子集 II - LeetCode](https://leetcode.com/problems/subsets-ii/)

#### 💻 **题目大意**

给你一个整数数组 `nums` ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 **不能** 包含重复的子集。返回的解集中，子集可以按 **任意顺序** 排列。

#### 💡 **解题思路**

比如输入 `nums = [1,2,2]`，函数的返回值应该是：`[ [],[1],[2],[1,2],[2,2],[1,2,2] ]`

就以 nums = [1,2,2] 为例，为了区别两个 2 是不同元素，后面我们写作 nums = [1,2,2']。

按照之前的思路画出子集的树形结构，显然，两条值相同的相邻树枝会产生重复：

```
[
    [],
    [1],[2],[2'],
    [1,2],[1,2'],[2,2'],
    [1,2,2']
]
```

可以看到，`[2] 与 [2']`、`[1,2] 与 [1,2']` 这两个结果出现了重复，所以需要进行剪枝，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：

![](../image/3-4-6.png)

体现在代码上，需要先进行排序，让相同的元素靠在一起，如果发现 `nums[i] == nums[i-1]`，则跳过。

代码和之前标准的子集问题的代码几乎相同，就是添加了排序和剪枝的逻辑。

#### 💎 **代码**

```javascript
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsetsWithDup = function (nums) {
	let res = [];
	let track = [];

	// 排序，以便在后续的步骤中去重
	nums.sort((a, b) => a - b);

	const backtrack = (start) => {
		res.push([...track]);

		for (let i = start; i < nums.length; i++) {
			// 出现了重复元素，跳过
			if (i > start && nums[i] == nums[i - 1]) {
				continue;
			}
			track.push(nums[i]);
			backtrack(i + 1);
			track.pop();
		}
	};

	backtrack(0);
	return res;
};
```

元素可重不可复选 - 组合

相关题目

📌 40. 组合总和 II - LeetCodeopen in new window

💻 题目大意

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。解集不能包含重复的组合。

💡 解题思路

组合问题和子集问题是等价的，说这是一个组合问题，其实换个问法就变成子集问题：请你计算 candidates 中所有和为 target 的子集。

对比子集问题的解法，只要额外用一个 sum 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题：

💎 代码

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
	let res = [];
	let track = [];
	let sum = 0;
	candidates.sort((a, b) => a - b);

	const backtrack = (start) => {
		if (sum == target) {
			res.push([...track]);
		}
		for (let i = start; i < candidates.length; i++) {
			// 若子集和超过 target ，则直接结束循环
			// 这是因为数组已排序，后边元素更大，子集和一定超过 target
			if (target - sum - candidates[i] < 0) {
				break;
			}
			if (i > start && candidates[i] == candidates[i - 1]) {
				continue;
			}
			track.push(candidates[i]);
			sum += candidates[i];
			backtrack(i + 1);
			track.pop();
			sum -= candidates[i];
		}
	};

	backtrack(0);
	return res;
};

#### 📌 [40. 组合总和 II - LeetCode](https://leetcode.com/problems/combination-sum-ii/)

#### 💻 **题目大意**

给定一个候选人编号的集合 `candidates` 和一个目标数 `target` ，找出 `candidates` 中所有可以使数字和为 `target` 的组合。`candidates` 中的每个数字在每个组合中只能使用 **一次** 。解集不能包含重复的组合。

#### 💡 **解题思路**

组合问题和子集问题是等价的，说这是一个组合问题，其实换个问法就变成子集问题：请你计算 `candidates` 中所有和为 `target` 的子集。

对比子集问题的解法，只要额外用一个 `sum` 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题：

#### 💎 **代码**

```javascript
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
	let res = [];
	let track = [];
	let sum = 0;
	candidates.sort((a, b) => a - b);

	const backtrack = (start) => {
		if (sum == target) {
			res.push([...track]);
		}
		for (let i = start; i < candidates.length; i++) {
			// 若子集和超过 target ，则直接结束循环
			// 这是因为数组已排序，后边元素更大，子集和一定超过 target
			if (target - sum - candidates[i] < 0) {
				break;
			}
			if (i > start && candidates[i] == candidates[i - 1]) {
				continue;
			}
			track.push(candidates[i]);
			sum += candidates[i];
			backtrack(i + 1);
			track.pop();
			sum -= candidates[i];
		}
	};

	backtrack(0);
	return res;
};
```

元素可重不可复选 - 排列

相关题目

📌 47. 全排列 II - LeetCodeopen in new window

💻 题目大意

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

💡 解题思路

排列问题的输入如果存在重复，比子集/组合问题稍微复杂一点。对比之前的标准全排列解法，需要增加两个点：

对 nums 进行排序；
添加一句额外的剪枝逻辑：i > 0 && nums[i] == nums[i - 1] && !used[i - 1]；

这个地方理解起来需要一些技巧，为了方便研究，依然把相同的元素用上标 ' 以示区别。

假设输入为 nums = [1,2,2']，标准的全排列算法会得出如下答案：

[
    [1,2,2'],[1,2',2],
    [2,1,2'],[2,2',1],
    [2',1,2],[2',2,1]
]

显然这个结果存在重复，比如 [1,2,2'] 和 [1,2',2] 应该只被算作同一个排列，但被算作了两个不同的排列。所以现在的关键在于，如何设计剪枝逻辑，把这种重复去除掉？答案是，保证相同元素在排列中的相对位置保持不变。

比如说 nums = [1,2,2'] 这个例子，保持排列中 2 一直在 2' 前面。这样的话，从上面 6 个排列中只能挑出 3 个排列符合这个条件：[ [1,2,2'],[2,1,2'],[2,2',1] ]，也就是正确答案。

进一步，如果 nums = [1,2,2',2'']，只要保证重复元素 2 的相对位置固定，比如说 2 -> 2' -> 2''，也可以得到无重复的全排列结果。

标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。反映到代码上，就是这个剪枝逻辑：

// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    // 如果前面的相邻相等元素没有用过，则跳过
    continue;
}
// 选择 nums[i]

当出现重复元素时，比如输入 nums = [1,2,2',2'']，2' 只有在 2 已经被使用的情况下才会被选择，同理，2'' 只有在 2' 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。

💎 代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function (nums) {
	let res = [];
	let track = [];
	let used = new Array(nums.length).fill(false);

	// 先排序，让相同的元素靠在一起
	nums.sort((a, b) => a - b);

	const backtrack = () => {
		if (track.length == nums.length) {
			res.push([...track]);
			return;
		}
		for (let i = 0; i < nums.length; i++) {
			// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
			if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
				continue;
			}
			track.push(nums[i]);
			used[i] = true;
			backtrack();
			track.pop();
			used[i] = false;
		}
	};

	backtrack();
	return res;
};

#### 📌 [47. 全排列 II - LeetCode](https://leetcode.com/problems/permutations-ii/)

#### 💻 **题目大意**

给定一个可包含重复数字的序列 `nums` ，**按任意顺序** 返回所有不重复的全排列。

#### 💡 **解题思路**

排列问题的输入如果存在重复，比子集/组合问题稍微复杂一点。对比之前的标准全排列解法，需要增加两个点：

1. 对 `nums` 进行排序；
2. 添加一句额外的剪枝逻辑：`i > 0 && nums[i] == nums[i - 1] && !used[i - 1]`；

这个地方理解起来需要一些技巧，为了方便研究，依然把相同的元素用上标 ' 以示区别。

假设输入为 `nums = [1,2,2']`，标准的全排列算法会得出如下答案：

```
[
    [1,2,2'],[1,2',2],
    [2,1,2'],[2,2',1],
    [2',1,2],[2',2,1]
]
```

显然这个结果存在重复，比如 `[1,2,2']` 和 `[1,2',2]` 应该只被算作同一个排列，但被算作了两个不同的排列。所以现在的关键在于，如何设计剪枝逻辑，把这种重复去除掉？答案是，**保证相同元素在排列中的相对位置保持不变。**

比如说 `nums = [1,2,2']` 这个例子，保持排列中 `2` 一直在 `2'` 前面。这样的话，从上面 `6` 个排列中只能挑出 `3` 个排列符合这个条件：`[ [1,2,2'],[2,1,2'],[2,2',1] ]`，也就是正确答案。

进一步，如果 `nums = [1,2,2',2'']`，只要保证重复元素 `2` 的相对位置固定，比如说 `2 -> 2' -> 2''`，也可以得到无重复的全排列结果。

**标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复**。反映到代码上，就是这个剪枝逻辑：

```javascript
// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    // 如果前面的相邻相等元素没有用过，则跳过
    continue;
}
// 选择 nums[i]
```

**当出现重复元素时，比如输入 `nums = [1,2,2',2'']`，`2'` 只有在 `2` 已经被使用的情况下才会被选择，同理，`2''` 只有在 `2'` 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。**

#### 💎 **代码**

```javascript
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function (nums) {
	let res = [];
	let track = [];
	let used = new Array(nums.length).fill(false);

	// 先排序，让相同的元素靠在一起
	nums.sort((a, b) => a - b);

	const backtrack = () => {
		if (track.length == nums.length) {
			res.push([...track]);
			return;
		}
		for (let i = 0; i < nums.length; i++) {
			// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
			if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
				continue;
			}
			track.push(nums[i]);
			used[i] = true;
			backtrack();
			track.pop();
			used[i] = false;
		}
	};

	backtrack();
	return res;
};
```

元素无重可复选 - 子集 / 组合

相关题目

📌 39. 组合总和 - LeetCodeopen in new window

💻 题目大意

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

比如输入 candidates = [1,2,3], target = 3，算法应该返回：[ [1,1,1],[1,2],[3] ]

💡 解题思路

这道题说是组合问题，实际上也是子集问题：candidates 的哪些子集的和为 target？

想解决这种类型的问题，也得回到回溯树上。

先思考，标准的子集/组合问题是如何保证不重复使用元素的？答案在于 backtrack 递归时输入的参数 start：

const backtrack = (start) => {
	for (let i = start; i < nums.length; i++) {
		// ...

		// 递归遍历下一层回溯树，注意参数
		backtrack(i + 1);

		// ...
	}
};

这个 i 从 start 开始，那么下一层回溯树就是从 start + 1 开始，从而保证 nums[start] 这个元素不会被重复使用。那么反过来，如果我想让每个元素被重复使用，我只要把 i + 1 改成 i 即可：

const backtrack = (start) => {
	for (let i = start; i < nums.length; i++) {
		// ...

		// 递归遍历下一层回溯树，注意参数
		backtrack(i);

		// ...
	}
};

这相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用：

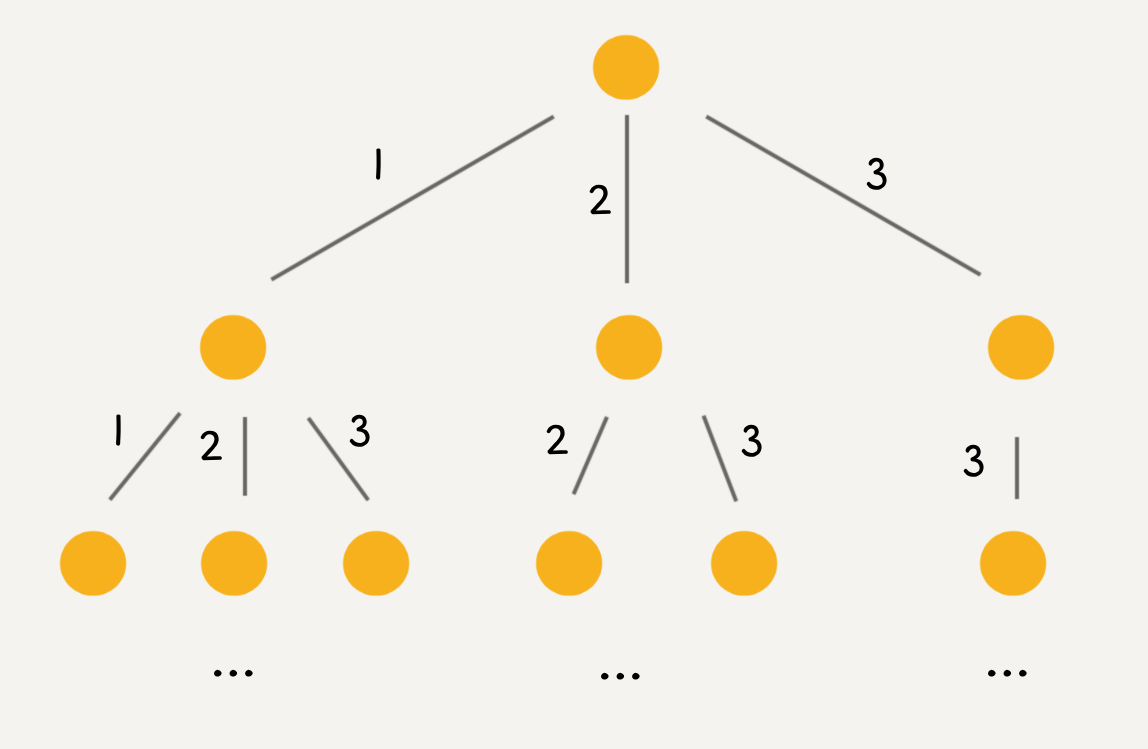
当然，这样这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 target 时就没必要再遍历下去了。

💎 代码

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	const len = candidates.length;
	let res = [];
	let track = [];
	let sum = 0;

	const backtrack = (start) => {
		// 满足条件
		if (sum == target) {
			res.push([...track]);
			return;
		}
		// 剪枝
		if (sum > target) {
			return;
		}
		for (let i = start; i < len; i++) {
			track.push(candidates[i]);
			sum += candidates[i];

			// 注意这里传入的参数是 i 而不是 i + 1，表示可以重复使用当前的数字
			backtrack(i);

			track.pop();
			sum -= candidates[i];
		}
	};
	backtrack(0);
	return res;
};

#### 📌 [39. 组合总和 - LeetCode](https://leetcode.com/problems/combination-sum/)

#### 💻 **题目大意**

给你一个 **无重复元素** 的整数数组 `candidates` 和一个目标整数 `target` ，找出 `candidates` 中可以使数字和为目标数 `target` 的 **所有** 不同组合 ，并以列表形式返回。你可以按 **任意顺序** 返回这些组合。

`candidates` 中的 **同一个** 数字可以 **无限制重复被选取** 。如果至少一个数字的被选数量不同，则两种组合是不同的。

比如输入 `candidates = [1,2,3], target = 3`，算法应该返回：`[ [1,1,1],[1,2],[3] ]`

#### 💡 **解题思路**

这道题说是组合问题，实际上也是子集问题：`candidates` 的哪些子集的和为 `target`？

想解决这种类型的问题，也得回到回溯树上。

先思考，标准的子集/组合问题是如何保证不重复使用元素的？答案在于 `backtrack` 递归时输入的参数 `start`：

```javascript
const backtrack = (start) => {
	for (let i = start; i < nums.length; i++) {
		// ...

		// 递归遍历下一层回溯树，注意参数
		backtrack(i + 1);

		// ...
	}
};
```

这个 `i` 从 `start` 开始，那么下一层回溯树就是从 `start + 1` 开始，从而保证 `nums[start]` 这个元素不会被重复使用。那么反过来，如果我想让每个元素被重复使用，我只要把 `i + 1` 改成 `i` 即可：

```javascript
const backtrack = (start) => {
	for (let i = start; i < nums.length; i++) {
		// ...

		// 递归遍历下一层回溯树，注意参数
		backtrack(i);

		// ...
	}
};
```

这相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用：

![](../image/3-4-7.png)

当然，这样这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 `target` 时就没必要再遍历下去了。

#### 💎 **代码**

```javascript
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
	const len = candidates.length;
	let res = [];
	let track = [];
	let sum = 0;

	const backtrack = (start) => {
		// 满足条件
		if (sum == target) {
			res.push([...track]);
			return;
		}
		// 剪枝
		if (sum > target) {
			return;
		}
		for (let i = start; i < len; i++) {
			track.push(candidates[i]);
			sum += candidates[i];

			// 注意这里传入的参数是 i 而不是 i + 1，表示可以重复使用当前的数字
			backtrack(i);

			track.pop();
			sum -= candidates[i];
		}
	};
	backtrack(0);
	return res;
};
```

元素无重可复选 - 排列

力扣上没有类似的题目，不妨自己算一下，nums 数组中的元素无重复且可复选的情况下，有哪些排列？

比如输入 nums = [1,2,3]，那么这种条件下的全排列共有 3^3 = 27 种：

[
  [1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
  [2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
  [3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]

标准的全排列算法利用 used 数组进行剪枝，避免重复使用同一个元素。如果允许重复使用元素的话，直接放飞自我，去除所有 used 数组的剪枝逻辑就行了。代码如下：

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteRepeat = function (nums) {
	let res = [];
	let track = [];

	const backtrack = () => {
		// base case，到达叶子节点
		if (track.length === nums.length) {
			res.push([...track]);
			return;
		}

		for (let i = 0; i < nums.length; i++) {
			track.push(nums[i]);
			backtrack();
			track.pop();
		}
	};

	backtrack();
	return res;
};

至此，排列、组合、子集问题的九种变化就都讲完了。

题号	标题	题解	标签	难度	力扣
46	全排列	[✓]	`数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
47	全排列 II	[✓]	`数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
37	解数独	[✓]	`数组` `哈希表` `回溯` `1+`	🔴	🀄️open in new window 🔗open in new window
22	括号生成	[✓]	`字符串` `动态规划` `回溯`	🟠	🀄️open in new window 🔗open in new window
17	电话号码的字母组合	[✓]	`哈希表` `字符串` `回溯`	🟠	🀄️open in new window 🔗open in new window
784	字母大小写全排列		`位运算` `字符串` `回溯`	🟠	🀄️open in new window 🔗open in new window
39	组合总和	[✓]	`数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
40	组合总和 II	[✓]	`数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
78	子集	[✓]	`位运算` `数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
90	子集 II	[✓]	`位运算` `数组` `回溯`	🟠	🀄️open in new window 🔗open in new window
473	火柴拼正方形		`位运算` `数组` `动态规划` `2+`	🟠	🀄️open in new window 🔗open in new window
1593	拆分字符串使唯一子字符串的数目最大	[✓]	`哈希表` `字符串` `回溯`	🟠	🀄️open in new window 🔗open in new window
1079	活字印刷		`哈希表` `字符串` `回溯` `1+`	🟠	🀄️open in new window 🔗open in new window
93	复原 IP 地址	[✓]	`字符串` `回溯`	🟠	🀄️open in new window 🔗open in new window
79	单词搜索	[✓]	`数组` `字符串` `回溯` `1+`	🟠	🀄️open in new window 🔗open in new window
679	24 点游戏		`数组` `数学` `回溯`	🔴	🀄️open in new window 🔗open in new window

3.4 回溯算法

# 3.4 回溯算法

# 回溯的定义

# 回溯的原理

# 回溯的框架套路

# 元素无重不可复选 - 子集

# 📌 78. 子集 - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素无重不可复选 - 组合

# 📌 77. 组合 - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素无重不可复选 - 排列

# 📌 46. 全排列 - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素可重不可复选 - 子集

# 📌 90. 子集 II - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素可重不可复选 - 组合

# 📌 40. 组合总和 II - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素可重不可复选 - 排列

# 📌 47. 全排列 II - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素无重可复选 - 子集 / 组合

# 📌 39. 组合总和 - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 元素无重可复选 - 排列

# 相关题目

3.4 回溯算法

回溯的定义

回溯的原理

回溯的框架套路

元素无重不可复选 - 子集

📌 78. 子集 - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素无重不可复选 - 组合

📌 77. 组合 - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素无重不可复选 - 排列

📌 46. 全排列 - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素可重不可复选 - 子集

📌 90. 子集 II - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素可重不可复选 - 组合

📌 40. 组合总和 II - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素可重不可复选 - 排列

📌 47. 全排列 II - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素无重可复选 - 子集 / 组合

📌 39. 组合总和 - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

元素无重可复选 - 排列

相关题目