1.2 复杂度分析
1.2 复杂度分析
想要学习数据结构与算法,首先要掌握一个最重要的概念——复杂度分析,它可以帮我们分析如何更省、更快地存储和处理数据。
时间复杂度
算法的 时间复杂度(time complexity) 是一个函数,它定性描述该算法的运行时间。用于评估执行程序所消耗的时间,可以估算出程序对处理器的使用程度。
时间复杂度常用大 O 符号表述,使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
相同大小的不同输入值仍可能造成算法的执行时间不同,因此我们通常使用算法的最坏情况复杂度,记为 T(n) ,定义为任何大小的输入 n 所需的最大执行时间。
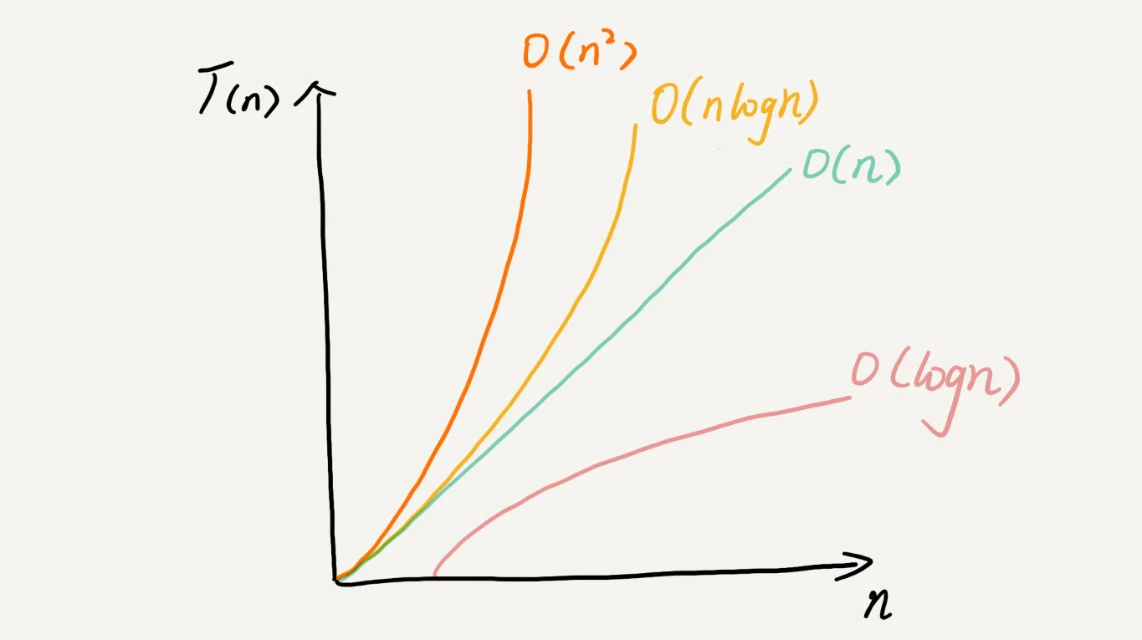
以下是一些最常用的 大 O 标记法 列表以及它们与不同大小输入数据的性能比较。

| 大 O 标记法 | 计算 10 个元素 | 计算 100 个元素 | 计算 1000 个元素 | 输入规模 n | 最大可接受值(约) |
|---|---|---|---|---|---|
| O(1) | 1 | 1 | 1 | 任意 | ✅ 超快 |
| O(log N) | 3 | 6 | 9 | 10^9 | ✅ 超快 |
| O(N) | 10 | 100 | 1000 | 10^8 | ✅ 可接受 |
| O(N log N) | 30 | 600 | 9000 | 10^6 - 10^7 | ✅ 一般可接受 |
| O(N^2) | 100 | 10^4 | 10^6 | 10^4 | ⚠️ 可能超时 |
| O(N^3) | 1000 | 10^6 | 10^9 | 10^3 | ⚠ 可能超时 |
| O(2^N) | 1024 | 1.26e+29 | 1.07e+301 | 20 | ❌ 极易超时 |
| O(N!) | 3628800 | 9.3e+157 | 4.02e+2567 | 10 | ❌ 极易超时 |
在遇到大规模输入时,尽量选择 低时间复杂度 的方法:
- 暴力搜索(O(2^n) 或 O(n!)):适用于
n ≤ 20 - 动态规划(O(n²)):适用于
n ≤ 10^4 - 分治 + 递归(O(n log n)):适用于
n ≤ 10^6 - 贪心、前缀和、滑动窗口、二分查找(O(n) 或 O(log n)):适用于
n ≤ 10^8
数据结构操作的复杂性
| 数据结构 | 连接 | 查找 | 插入 | 删除 | 备注 |
|---|---|---|---|---|---|
| 数组 | 1 | n | n | n | |
| 栈 | n | n | 1 | 1 | |
| 队列 | n | n | 1 | 1 | |
| 链表 | n | n | 1 | 1 | |
| 哈希表 | - | n | n | n | 在完全哈希函数情况下,复杂度是 O(1) |
| 二分查找树 | n | n | n | n | 在平衡树情况下,复杂度是 O(log(n)) |
| B 树 | log(n) | log(n) | log(n) | log(n) | |
| 红黑树 | log(n) | log(n) | log(n) | log(n) | |
| AVL 树 | log(n) | log(n) | log(n) | log(n) | |
| 布隆过滤器 | - | 1 | 1 | - | 存在一定概率的判断错误(误判成存在) |
数组排序算法的复杂性
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | in-place | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | in-place | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | in-place | 稳定 |
| 希尔排序 | O(nlogn) | O(nlog^2n) | O(nlog^2n) | O(1) | in-place | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | out-place | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | in-place | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | in-place | 不稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n^2) | O(n+k) | out-place | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | out-place | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | out-place | 稳定 |
分析复杂度的一些规则
- 多个时间复杂度相加,如果都是与 n 相关,则取取复杂度高的那一个,例如:
O(nlogn + n) = O(nlogn),O(nlogn + n^2) = O(n^2)。 - 多个时间复杂度相加,如果其中有些项的复杂度和 n 不相关则不能忽略任何项,例如:
O(AlogA + B),O(AlogA + B^2) - 两个循环依次执行,则取复杂度高的那个,嵌套多个循环则需要累乘复杂度。
一个时间复杂度分析的例子:
有一个字符串数组,将数组中的每个字符串按照字母排序,然后在将整个字符串数组按照字典顺序排序。求整个操作的时间复杂度。
我们来分析一下,假设最长字符串的长度是 s,数组中有 n 个字符串。
对每个字符串排序
O(slogs),将数组中的每个字符串按照字母排序O(n * slogs);将整个字符串数组按字典排序
O(s * nlogn);所以最后的时间复杂度是
O(n * slogs) + O(s * nlogn) = O(nslogs + nslogn) = O(ns * (logs+logn))
时间复杂度优化
- 采用更好的算法:举例:
1+2+3...n从1~n求和,直接循环法,for i->n: sum+=i,我们也可以用求和公式:n(n+1)/2;有些问题可以用二分查找等。 - 空间换时间,比如用 set 或 map 加快查找的速度,用二叉搜索树或者字典树加快字符串的搜索。
空间复杂度
空间复杂度(Space Complexity) 指的是算法在运行过程中所占存储空间的大小,依然使用大 O 来表示。用于评估执行程序所占用的内存空间,可以估算出程序对计算机内存的使用程度。
常见的空间复杂度
- 一维数组空间,如果存储了 n 个元素,空间复杂度
O(n); - 二维数组空间,总共有 n 个数组,每个数组存储了 n 个元素,空间复杂度
O(n^2); - 常数空间复杂度
O(1);
