2.1 数组

数组的定义

定义

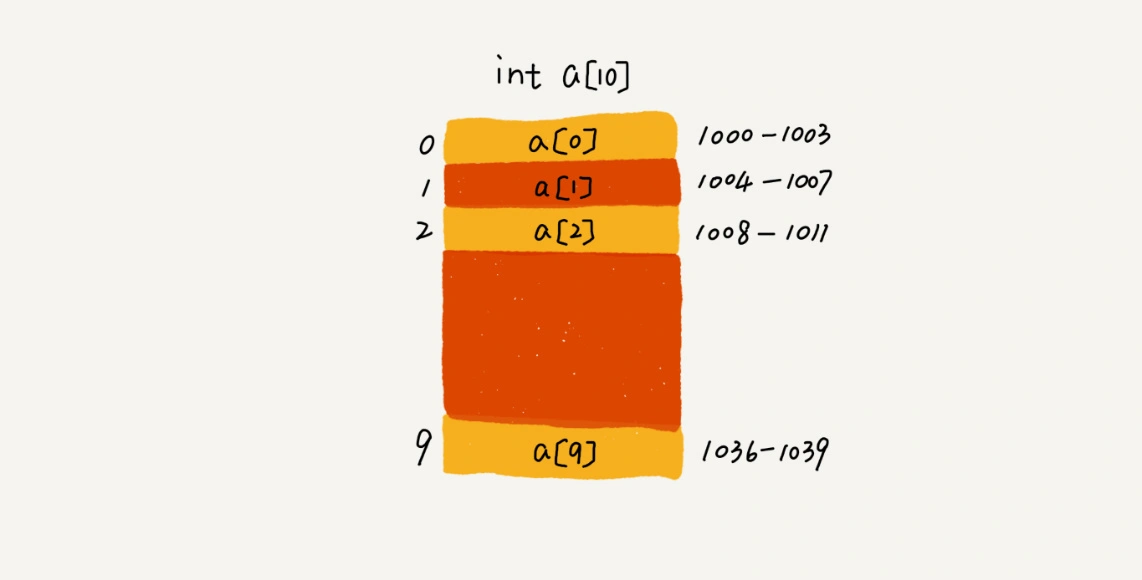
数组（Array） 是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

但在 JavaScript 里，数组中可以保存不同类型的值（大多数语言都没这个能力）。但我们还是要遵守最佳实践，别这么做。

// 一维数组：
// 数组的每一个元素是一个数据类型
[1, 2, 3]

// 二维数组：
// 数组的每一个元素是一个一维数组
[["a", "b", "c"], [1, 2, 3], 123]

// 三维数组：
// 数组的每一个元素是一个二维数组
[
  [
    ["a", "b", "c"],
    [1, 2, 3],
  ],
  [
    ["a", "b", "c"],
    [1, 2, 3],
  ],
]

我们还可以从两个方面来解释一下数组的定义。

• 「线性表」
• 「连续的内存空间」

线性表与非线性表

定义

线性表（Linear List） 就是数据排成像一条线一样的结构，线性表上的数据元素都是相同类型。每个线性表上的数据最多只有前和后两个方向。

数组、链表、队列、栈都是是线性表结构。

线性表有两种存储结构：「顺序存储结构」和「链式存储结构」。

其中，「顺序存储结构」是指占用的内存空间是连续的，相邻数据元素之间，物理内存上的存储位置也相邻。

数组也是采用了顺序存储结构，并且存储的数据都是相同类型的。

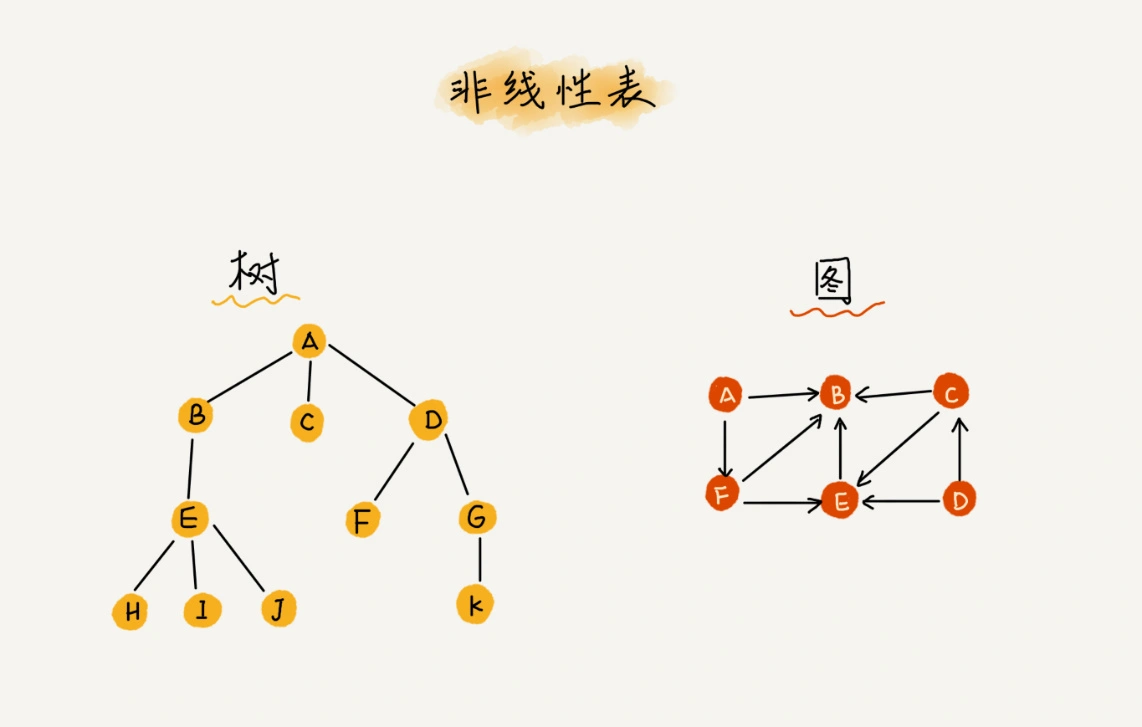
与它相对立的是非线性表，比如二叉树、堆、图等。

在非线性表中，数据之间并不是简单的前后关系。

数组的操作

数据结构的操作一般涉及到增、删、改、查共 4 种情况，下面我们一起来看一下数组的这 4 种基本操作。

1. 访问和查找元素

因为数组有连续的内存空间和相同类型的数据，所以数组支持 “随机访问”。

但这两个限制也让数组的很多操作变得非常低效，比如在数组中删除、插入一个数据，为了内存数据的保证连续性，就需要做大量的数据搬移工作。

在面试的时候，面试官常常会问数组和链表的区别？很多人都回答说，“链表适合插入、删除，时间复杂度 O(1)；数组适合查找，查找时间复杂度为 O(1)”。实际上，这种表述是不准确的。

数组适合查找操作，但是查找的时间复杂度并不为 O(1)。即便是排好序的数组，用二分查找，时间复杂度也是 O(logn)。

所以，正确的表述应该是，数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)。

2. 修改元素

• 修改指定索引位置的元素 array.splice(index, 1, item)

  let myArray3 = [1, 2, 3, 4, 5, 6];
  // 修改 索引 1 的位置的元素为 AA
  myArray2.splice(1, 1, 'AA');
  console.log(myArray3); //--> [1, "AA", 3, 4, 5, 6]
  

• 修改指定索引位置的几个元素 array.splice(index, number, item)

  let myArray4 = [1, 2, 3, 4, 5, 6, 7];
  // 在 索引 2 的位置起，修改两个元素为 AA BB
  myArray2.splice(2, 2, 'AA', 'BB');
  console.log(myArray3); //--> [1, 2, "AA", "BB", 5, 6, 7]
  

改变元素的操作跟访问元素操作类似，访问操作不依赖于数组中元素个数，因此，「改变元素」的时间复杂度为 O(1)。

3. 插入元素

• 添加一个元素到数组的最后位置 array.push(item)
• 在数组首位插入一个元素 array.unshift(item)
• 在指定索引位置插入元素 array.splice(index, 0, item)

  splice() 第二个参数为 0 时，表示插入数据。

  let myArray = [1, 2, 3];
  // 在 索引 0 的位置，插入 A
  myArray.splice(0, 0, 'A');
  console.log(myArray); //--> ['A', 1, 2, 3]
  

假设数组的长度为 n，将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾给新来的数据，要将第 k ～ n 这部分的元素都顺序地往后挪一位。

• 如果在数组的末尾插入元素，不需要移动数据，时间复杂度为 O(1)。
• 但如果在数组的开头插入元素，那所有的数据都要依次往后移动一位，所以最坏时间复杂度是O(n)。
• 因为每个位置插入元素的概率一样，所以平均情况时间复杂度为(1 + 2 + … + n) / n = O(n)。

如果数组中的数据是有序的，在插入新元素时就必须搬移 k 之后的数据。但是，如果数组中存储的数据并没有任何规律，将某个新元素插入到第 k 个位置时，为了避免大规模的数据搬移，有一个简单的办法就是，直接将第 k 位的数据搬移到数组元素的最后，把新的元素直接放入第 k 个位置。

例如：数组 a 中存储了如下 5 个元素：a，b，c，d，e。要将元素 x 插入到第 3 个位置。只需将 c 放入到 a[5]，将 a[2]赋值为 x 即可。最后数组中的元素如下： a，b，x，d，e，c。

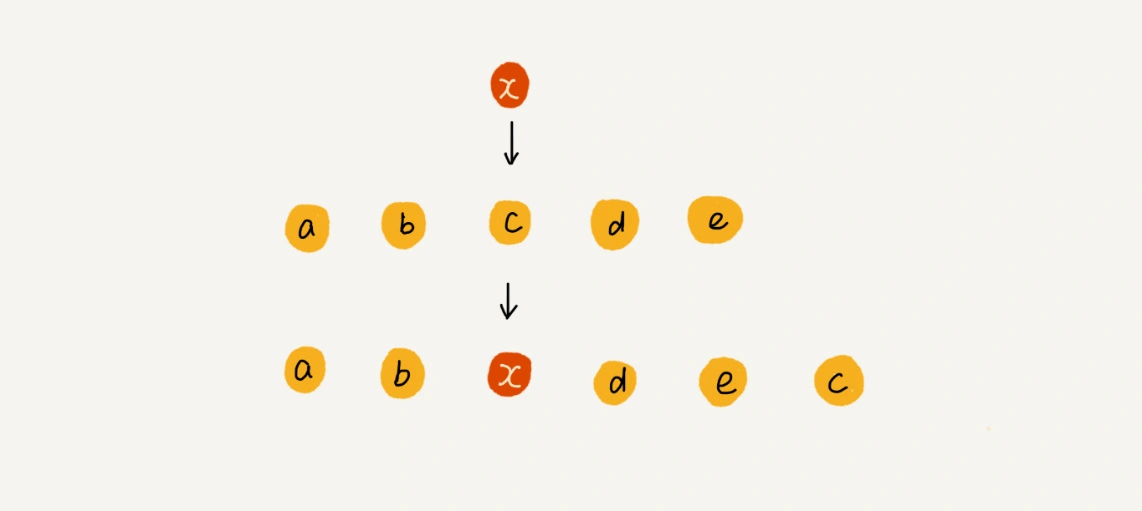
利用这种处理技巧，在特定场景下，在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)。这个处理思想在快排中也会用到。

4. 删除元素

• 删除数组最后的元素 array.pop()
• 删除数组首位的元素 array.shift()
• 删除指定索引位置的元素 array.splice(start, deleteCount) 例如：

  let myArray2 = [1, 2, 3, 4, 5];
  // 删除索引 3 位置起，2 个元素
  myArray2.splice(3, 2);
  console.log(myArray2); //--> [1, 2, 3]
  

跟插入数据类似，如果我们要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。

和插入类似：

• 如果删除数组末尾的数据，则最好情况时间复杂度为 O(1)；
• 如果删除开头的数据，则最坏情况时间复杂度为 O(n)；
• 平均情况时间复杂度也为 O(n)。

实际上，在某些特殊场景下，并不一定非得追求数组中数据的连续性。如果每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，再触发执行一次真正的删除操作，就可以大大减少了删除操作导致的数据搬移。这也是JVM 标记清除垃圾回收算法的核心思想。

相关题目

数组操作

题号	标题	题解	标签	难度	力扣
189	轮转数组	[✓]	数组 数学 双指针	🟠	🀄️ 🔗
66	加一	[✓]	数组 数学	🟢	🀄️ 🔗
724	寻找数组的中心下标	[✓]	数组 前缀和	🟢	🀄️ 🔗
485	最大连续 1 的个数	[✓]	数组	🟢	🀄️ 🔗
238	除自身以外数组的乘积	[✓]	数组 前缀和	🟠	🀄️ 🔗

二维数组

题号	标题	题解	标签	难度	力扣
498	对角线遍历	[✓]	数组 矩阵 模拟	🟠	🀄️ 🔗
48	旋转图像	[✓]	数组 数学 矩阵	🟠	🀄️ 🔗
73	矩阵置零	[✓]	数组 哈希表 矩阵	🟠	🀄️ 🔗
54	螺旋矩阵	[✓]	数组 矩阵 模拟	🟠	🀄️ 🔗
59	螺旋矩阵 II	[✓]	数组 矩阵 模拟	🟠	🀄️ 🔗
289	生命游戏	[✓]	数组 矩阵 模拟	🟠	🀄️ 🔗