2.4 队列

队列的定义

定义

队列（Queue） ：一种线性表数据结构，是一种只允许在表的一端进行插入操作，而在表的另一端进行删除操作的线性表。

先进者先出，这就是典型的“队列”。你可以把它想象成排队买票，先来的先买，后来的人只能站末尾，不允许插队。

队列跟栈一样，也是一种操作受限的线性表数据结构，栈只支持两个基本操作：入栈 push() 和出栈 pop()。队列最基本的操作也是两个：入队 enQueue()，放一个数据到队列尾部；出队 deQueue()，从队列头部取一个元素。

我们把队列中允许插入的一端称为 队尾（rear）；把允许删除的另一端称为 队头（front）。当表中没有任何数据元素时，称之为 空队。

我们可以从两个方面来解释一下队列的定义：

• 「线性表」

  队列首先是一个线性表，队列中元素具有前驱后继的线性关系。队列中元素按照 a1,a2,...,an 的次序依次入队。队头元素为 a1，队尾元素为 an。

• 「先进先出原则」

  元素进入队列或者退出队列是按照 「先进先出（First In First Out）」 的原则进行的，最先进入队列的元素在队头，最后进入队列的元素在队尾。每次从队列中删除的总是队头元素，即最先进入队列的元素。

队列的实现

跟栈一样，队列可以用数组来实现，也可以用链表来实现。

用数组实现的栈叫作顺序栈，用链表实现的栈叫作链式栈。

同样，用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

顺序队列

class ArrayQueue {
	constructor() {
		this._queue = [];
	}
	// 入队
	enQueue(data) {
		this._queue.push(data);
	}
	// 出队
	deQueue() {
		if (this.isEmpty()) {
			console.log('This queue is empty');
			return null;
		}
		return this._queue.shift();
	}
	// 判断是否为空队
	isEmpty() {
		return this._queue.length === 0;
	}
	// 查看队头元素
	front() {
		if (this.isEmpty()) {
			console.log('This queue is empty');
			return null;
		}
		return this._queue[0];
	}
	// 查看队尾元素
	rear() {
		if (this.isEmpty()) {
			console.log('This queue is empty');
			return null;
		}
		return this._queue[this.count() - 1];
	}
	// 清空队列
	clear() {
		delete this._queue;
		this._queue = [];
	}
	// 打印队列
	print() {
		console.log(this._queue);
	}
	// 获取队列中元素的数量
	count() {
		return this._queue.length;
	}
	// 将队列中元素以字符串形式返回
	toString() {
		return this._queue.join(',');
	}
}

👉 查看代码测试 👈

const queue = new ArrayQueue();
queue.enQueue(1);
queue.enQueue(2);
queue.enQueue(3);
queue.print(); // output: [1, 2, 3]
console.log(queue.front()); // output: 1
console.log(queue.rear()); // output: 3
queue.deQueue();
queue.print(); // output: [2, 3]
console.log(queue.count()); // output: 2
console.log(queue.isEmpty()); // output: false
console.log(queue.toString()); // output: 2,3

---

链式队列

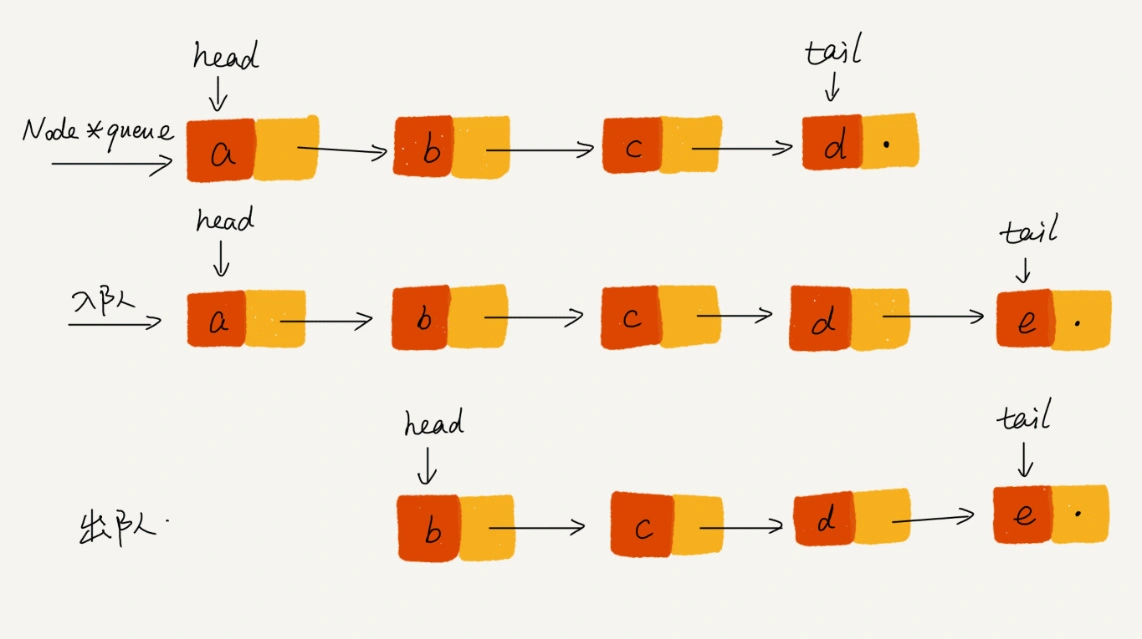
基于链表的实现，需要两个指针： head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。

如图所示：

• 入队时：tail.next= new_node, tail = tail.next
• 出队时：head = head.next

class Node {
	constructor(data) {
		this.data = data; // 节点中的数据
		this.next = null; // 下一个节点
	}
}
class LinkedListQueue {
	constructor() {
		this.head = null;
		this.tail = null;
		this.length = 0;
	}
	// 入队
	enQueue(data) {
		const node = new Node(data);
		if (this.isEmpty()) {
			this.head = node;
			this.tail = node;
		} else {
			this.tail.next = node;
			this.tail = this.tail.next;
		}
		this.length++;
	}
	// 出队
	deQueue() {
		if (this.isEmpty()) return null;
		let cur = this.head;
		this.head = this.head.next;
		this.length--;
		return cur;
	}
	// 判断是否为空队
	isEmpty() {
		return this.length === 0;
	}
	// 查看队头元素
	front() {
		if (this.isEmpty()) {
			console.log('This queue is empty');
			return null;
		}
		return this.head.data;
	}
	// 查看队尾元素
	rear() {
		if (this.isEmpty()) {
			console.log('This queue is empty');
			return null;
		}
		return this.tail.data;
	}
	// 清空队列
	clear() {
		this.tail = null;
		this.head.next = null;
		this.head = null;
		this.length = 0;
	}
	// 打印队列
	print() {
		console.log(this.head);
	}
	// 获取队列中元素的数量
	count() {
		return this.length;
	}
	// 将队列中元素以字符串形式返回
	toString() {
		let res = [];
		let prev = this.head;
		while (prev) {
			res.push(prev.data);
			prev = prev.next;
		}
		return res.join(',');
	}
}

👉 查看代码测试 👈

const queue = new LinkedListQueue();
queue.enQueue(1);
queue.enQueue(2);
queue.enQueue(3);
queue.deQueue();
queue.print();
// output: Node {data: 2, next: Node {data: 3, next: null}}

console.log(queue.count()); // output: 2
console.log(queue.front()); // output: 2
console.log(queue.rear()); // output: 3
console.log(queue.isEmpty()); // output: false
console.log(queue.toString()); // output: 2,3

---

循环队列

定义

循环队列（Circular Queue） 是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则，并且队尾被连接在队首之后，以形成一个循环。它也被称为“环形缓冲器”。

在基于数组实现的顺序队列中，由于出队操作总是删除当前的队头元素，将 front 进行右移，而插入操作又总是在队尾进行。经过不断的出队、入队操作，队列的变化就像是使队列整体向右移动。

当队尾指针指向最右边时，即使在队列前面仍有空闲空间，也无法继续往队列中添加数据了，之前因为出队操作而产生空余位置没有利用上，这就造成了 假溢出 问题。

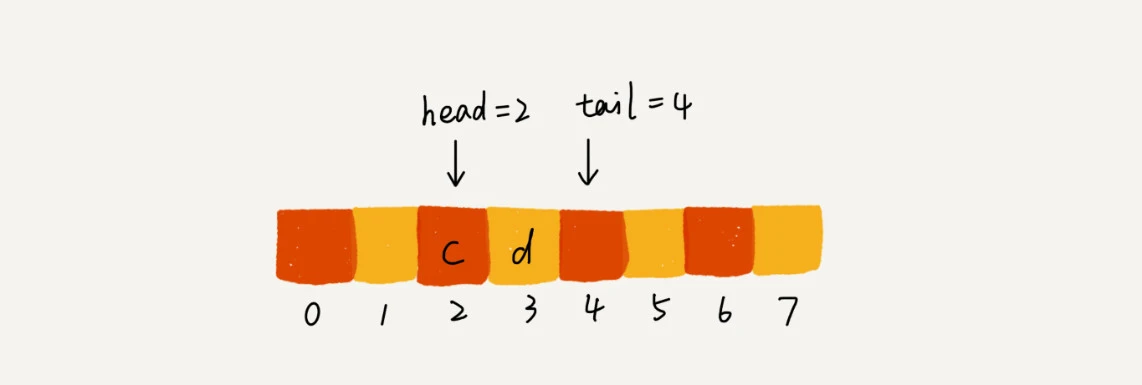
为了解决这个问题，我们可以将队列想象成为头尾相连的循环表。原本数组是有头有尾的，是一条直线。把首尾相连之后，被扳成了一个环，利用数学中的求模运算，我们能使用这些前面的空闲空间去存储新的值。

相关题目

📌 622. 设计循环队列 - LeetCode

💻 题目大意

设计循环队列，支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k ；
• Front: 从队首获取元素。如果队列为空，返回 -1 ；
• Rear: 获取队尾元素。如果队列为空，返回 -1 ；
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真；
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真；
• isEmpty(): 检查循环队列是否为空；
• isFull(): 检查循环队列是否已满；

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4

说明：

• 所有的值都在 0 至 1000 的范围内；
• 操作数将在 1 至 1000 的范围内；
• 请不要使用内置的队列库。

💎 代码

/**
 * @param {number} k
 */
var MyCircularQueue = function (k) {
	this.queue = new Array(k);
	this.head = 0;
	this.tail = 0;
	this.size = k;
};

/**
 * @param {number} value
 * @return {boolean}
 */
MyCircularQueue.prototype.enQueue = function (value) {
	if (this.isFull()) return false;
	this.queue[this.tail] = value;
	// 将 tail 指向队尾的下一个空间
	this.tail = (this.tail + 1) % this.size;
	return true;
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.deQueue = function () {
	if (this.isEmpty()) return false;
	this.queue[this.head] = null;
	// 将 head 指向新的队头
	this.head = (this.head + 1) % this.size;
	return true;
};

/**
 * @return {number}
 */
MyCircularQueue.prototype.Front = function () {
	return this.isEmpty() ? -1 : this.queue[this.head];
};

/**
 * @return {number}
 */
MyCircularQueue.prototype.Rear = function () {
	// 因为 tail 指向队尾的下一个空间，所以要分情况处理
	// 若 tail == 0，那队尾应该在 size - 1
	// 其他情况，队尾在 tail - 1
	let index = this.tail === 0 ? this.size - 1 : this.tail - 1;
	return this.isEmpty() ? -1 : this.queue[index];
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.isEmpty = function () {
	// head == tail 时，有两种情况
	// 一种是队列为空，此时 queue[head] 为null
	// 一种是队列满了，此时 queue[head] 有值
	return this.head === this.tail && !this.queue[this.head];
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.isFull = function () {
	return this.head === this.tail && !!this.queue[this.head];
};

#### 📌 [622. 设计循环队列 - LeetCode](https://2xiao.github.io/leetcode-js/problem/0622.html)

#### 💻 **题目大意**

设计循环队列，支持如下操作：

- `MyCircularQueue(k)`: 构造器，设置队列长度为 `k` ；
- `Front`: 从队首获取元素。如果队列为空，返回 `-1` ；
- `Rear`: 获取队尾元素。如果队列为空，返回 `-1` ；
- `enQueue(value)`: 向循环队列插入一个元素。如果成功插入则返回真；
- `deQueue()`: 从循环队列中删除一个元素。如果成功删除则返回真；
- `isEmpty()`: 检查循环队列是否为空；
- `isFull()`: 检查循环队列是否已满；

**示例**：

```javascript
MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4
```

**说明**：

- 所有的值都在 `0` 至 `1000` 的范围内；
- 操作数将在 `1` 至 `1000` 的范围内；
- 请不要使用内置的队列库。

#### 💎 代码

```javascript
/**
 * @param {number} k
 */
var MyCircularQueue = function (k) {
	this.queue = new Array(k);
	this.head = 0;
	this.tail = 0;
	this.size = k;
};

/**
 * @param {number} value
 * @return {boolean}
 */
MyCircularQueue.prototype.enQueue = function (value) {
	if (this.isFull()) return false;
	this.queue[this.tail] = value;
	// 将 tail 指向队尾的下一个空间
	this.tail = (this.tail + 1) % this.size;
	return true;
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.deQueue = function () {
	if (this.isEmpty()) return false;
	this.queue[this.head] = null;
	// 将 head 指向新的队头
	this.head = (this.head + 1) % this.size;
	return true;
};

/**
 * @return {number}
 */
MyCircularQueue.prototype.Front = function () {
	return this.isEmpty() ? -1 : this.queue[this.head];
};

/**
 * @return {number}
 */
MyCircularQueue.prototype.Rear = function () {
	// 因为 tail 指向队尾的下一个空间，所以要分情况处理
	// 若 tail == 0，那队尾应该在 size - 1
	// 其他情况，队尾在 tail - 1
	let index = this.tail === 0 ? this.size - 1 : this.tail - 1;
	return this.isEmpty() ? -1 : this.queue[index];
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.isEmpty = function () {
	// head == tail 时，有两种情况
	// 一种是队列为空，此时 queue[head] 为null
	// 一种是队列满了，此时 queue[head] 有值
	return this.head === this.tail && !this.queue[this.head];
};

/**
 * @return {boolean}
 */
MyCircularQueue.prototype.isFull = function () {
	return this.head === this.tail && !!this.queue[this.head];
};
```

优先队列

定义

优先队列（Priority Queue） ：一种特殊的队列。在优先队列中，元素被赋予优先级，当访问队列元素时，具有最高优先级的元素最先删除。

优先队列与普通队列最大的不同点在于 出队顺序。

• 普通队列的出队顺序跟入队顺序相关，符合 先进先出（First in, First out） 的规则；
• 优先队列的出队顺序跟入队顺序无关，优先队列是按照元素的优先级来决定出队顺序的。优先级高的元素优先出队，优先级低的元素后出队。优先队列符合 最高级先出（First in, Largest out） 的规则；

优先队列的实现方式有很多种，除了使用 数组 实现（顺序存储）与 链表 实现（链式存储）之外，最常用的是使用 二叉堆 实现。

数组实现

数组按优先级升序排序（ priority 值越小，优先级越高），入队需要遍历整个数组，插入到合适的位置，时间复杂度为 O(n)。出队直接返回队头元素，并删除队头元素，时间复杂度为 O(1)；

// 优先队列内部的元素类
class QueueElement {
	constructor(data, priority) {
		this.data = data;
		this.priority = priority;
	}
}

// 优先队列类（继承 ArrayQueue 类）
class PriorityQueue extends ArrayQueue {
	constructor() {
		super();
	}

	// 入队，将元素按优先级加入到队列中
	// 重写 enQueue()
	enQueue(data, priority) {
		// 根据传入的元素，创建 QueueElement 对象
		const queueElement = new QueueElement(data, priority);

		// 判断队列是否为空
		if (this.isEmpty()) {
			// 如果为空，不用判断优先级，直接添加
			this._queue.push(queueElement);
		} else {
			// 定义一个变量记录是否成功添加了新元素
			let added = false;

			for (let i = 0; i < this._queue.length; i++) {
				// 让新插入的元素进行优先级比较，priority 值越小，优先级越大
				if (queueElement.priority < this._queue[i].priority) {
					// 在指定的位置插入元素
					this._queue.splice(i, 0, queueElement);
					added = true;
					break;
				}
			}

			// 如果遍历完所有元素，优先级都大于新插入的元素，就将新插入的元素插入到最后
			if (!added) {
				this._queue.push(queueElement);
			}
		}
	}
	// 将队列中元素以字符串形式返回
	// 重写 toString()
	toString() {
		let res = [];
		for (let item of this._queue) {
			res.push(item.data + '-' + item.priority);
		}
		return res.join(',');
	}
	// 其他属性继承 ArrayQueue 类的
}

👉 查看代码测试 👈

const priorityQueue = new PriorityQueue();

priorityQueue.enQueue('A', 10);
priorityQueue.enQueue('B', 15);
priorityQueue.enQueue('C', 11);
priorityQueue.enQueue('D', 20);
priorityQueue.enQueue('E', 18);
priorityQueue.print();
// output:
// [QueueElement {data: 'A', priority: 10},
//   QueueElement {data: 'C', priority: 11},
//   QueueElement {data: 'B', priority: 15},
//   QueueElement {data: 'E', priority: 18},
//   QueueElement {data: 'D', priority: 20}]

priorityQueue.deQueue();
priorityQueue.deQueue();
priorityQueue.print();
// output:
// [QueueElement {data: 'B', priority: 15},
//   QueueElement {data: 'E', priority: 18},
//   QueueElement {data: 'D', priority: 20}]

console.log(priorityQueue.isEmpty()); // output: false
console.log(priorityQueue.count()); // output: 3
console.log(priorityQueue.toString()); // output: B-15,E-18,D-20

链表实现

链表中的元素按照优先级排序，入队操作需要为待插入元素创建节点，并在链表中找到合适的插入位置，时间复杂度为 O(n)。出队操作直接返回链表队头元素，并删除队头元素，时间复杂度为 O(1)；

class Node {
	constructor(data, priority) {
		this.data = data;
		this.next = null;
		this.priority = priority;
	}
}
// 优先队列类（继承 LinkedListQueue 类）
class PriorityQueue extends LinkedListQueue {
	constructor() {
		super();
	}
	// 入队，将元素按优先级加入到队列中
	// 重写 enQueue()
	enQueue(data, priority) {
		const node = new Node(data, priority);
		if (this.isEmpty()) {
			this.head = node;
			this.tail = node;
		} else {
			let prev = new Node(0, 0);
			prev.next = this.head;
			// 定义一个变量记录是否成功添加了新元素
			let added = false;
			for (let i = 0; i < this.length; i++) {
				if (node.priority < prev.next.priority && !added) {
					let temp = prev.next;
					prev.next = node;
					node.next = temp;
					prev = node;
					added = true;
				}
				prev = prev.next;
				this.tail = prev;
			}

			// 如果遍历完所有元素，优先级都大于新插入的元素，就将新插入的元素插入到最后
			if (!added) {
				this.tail.next = node;
				this.tail = this.tail.next;
			}
		}
		this.length++;
	}
	// 将队列中元素以字符串形式返回
	toString() {
		let res = [];
		let prev = this.head;
		while (prev) {
			res.push(prev.data + '-' + prev.priority);
			prev = prev.next;
		}
		return res.join(',');
	}
	// 其他属性都继承 LinkedListQueue 类
}

👉 查看代码测试 👈

const priorityQueue = new PriorityQueue();

priorityQueue.enQueue('A', 10);
priorityQueue.enQueue('B', 15);
priorityQueue.enQueue('C', 11);
priorityQueue.enQueue('D', 20);
priorityQueue.enQueue('E', 18);
priorityQueue.print();
// output:
// Node {data: 'A', priority: 10, next: Node {
//         data: 'C', priority: 11, next: Node {
//           data: 'B', priority: 15, next: Node {
//             data: 'E', priority: 18, next: Node {
//               data: 'D', priority: 20, next: null }}}}}

priorityQueue.deQueue();
priorityQueue.deQueue();
priorityQueue.print();
// output:
// Node {data: 'B', priority: 15, next: Node {
//         data: 'E', priority: 18, next: Node {
//           data: 'D', priority: 20, next: null }}}

console.log(priorityQueue.isEmpty()); // output: false
console.log(priorityQueue.count()); // output: 3
console.log(priorityQueue.toString()); // output: B-15,E-18,D-20

二叉堆实现

堆是一种特殊的二叉树，关于堆的知识点，可以详见：2.7 堆。

Java 中的优先队列就是基于堆实现的，是一个小顶堆。往优先队列中插入一个元素，就相当于往堆中插入一个元素；从优先队列中取出优先级最高的元素，就相当于取出堆顶元素。

构建一个二叉堆结构，二叉堆按照优先级进行排序。入队操作就是将元素插入到二叉堆中合适位置，时间复杂度为 O(logn)。出队操作则返回二叉堆中优先级最大节点并删除，时间复杂度也是 O(logn)；

class PriorityQueue extends ArrayQueue {
	constructor() {
		super();
	}

	enQueue(data, priority) {
		const queueElement = new QueueElement(data, priority);
		this._queue.push(queueElement);
		this._heapifyUp();
	}

	deQueue() {
		if (this._queue.length === 0) {
			return null;
		}

		const highestPriority = this._queue[0];
		const last = this._queue.pop();

		if (this._queue.length > 0) {
			this._queue[0] = last;
			this._heapifyDown(0);
		}

		return highestPriority;
	}

	_heapifyUp() {
		let cur = this._queue.length - 1;

		while (cur > 0) {
			const parent = Math.floor((cur - 1) / 2);
			if (this._queue[cur].priority > this._queue[parent].priority) {
				[this._queue[cur], this._queue[parent]] = [
					this._queue[parent],
					this._queue[cur]
				];
				cur = parent;
			} else {
				break;
			}
		}
	}

	_heapifyDown(index) {
		let cur = 0;

		while (true) {
			const leftChild = 2 * cur + 1;
			const rightChild = 2 * cur + 2;
			let next = null;

			if (
				leftChild < this._queue.length &&
				this._queue[leftChild].priority > this._queue[cur].priority
			) {
				next = leftChild;
			}

			if (
				rightChild < this._queue.length &&
				this._queue[rightChild].priority > this._queue[cur].priority
			) {
				next =
					this._queue[rightChild].priority > this._queue[leftChild].priority
						? rightChild
						: leftChild;
			}

			if (
				next !== null &&
				this._queue[cur].priority < this._queue[next].priority
			) {
				[this._queue[cur], this._queue[next]] = [
					this._queue[next],
					this._queue[cur]
				];
				cur = next;
			} else {
				break;
			}
		}
	}
	// 将队列中元素以字符串形式返回
	// 重写 toString()
	toString() {
		let res = [];
		for (let item of this._queue) {
			res.push(item.data + '-' + item.priority);
		}
		return res.join(',');
	}
	// 其他属性都继承 ArrayQueue 类
}

👉 查看代码测试 👈

const priorityQueue = new PriorityQueue();

priorityQueue.enQueue('A', 10);
priorityQueue.enQueue('B', 15);
priorityQueue.enQueue('C', 11);
priorityQueue.enQueue('D', 20);
priorityQueue.enQueue('E', 18);
priorityQueue.toString();
// output: 'D-20,E-18,C-11,A-10,B-15'

priorityQueue.deQueue();
priorityQueue.deQueue();
priorityQueue.toString();
// output: 'B-15,A-10,C-11'

console.log(priorityQueue.isEmpty()); // output: false
console.log(priorityQueue.count()); // output: 3

时间复杂度

三种结构实现的优先队列，入队操作和出队操作的时间复杂度总结：

时间复杂度	入队	出队
数组	O(n)	O(1)
链表	O(n)	O(1)
二叉堆	O(logn)	O(logn)

优先队列的应用

优先队列的应用场景非常多，比如：

• 数据压缩：赫夫曼编码算法；
• 最短路径算法：Dijkstra 算法；
• 最小生成树算法：Prim 算法；
• 任务调度器：根据优先级执行系统任务；
• 事件驱动仿真：顾客排队算法；
• 排序问题：查找第 k 个最小元素；

相关题目

队列基础题目

题号	标题	题解	标签	难度	力扣
622	设计循环队列	[✓]	设计 队列 数组 1+	🟠	🀄️ 🔗
346	数据流中的移动平均值 🔒	[✓]	设计 队列 数组 1+	🟢	🀄️ 🔗
225	用队列实现栈	[✓]	栈 设计 队列	🟢	🀄️ 🔗

优先队列

题号	标题	题解	标签	难度	力扣
703	数据流中的第 K 大元素	[✓]	树 设计 二叉搜索树 3+	🟢	🀄️ 🔗
347	前 K 个高频元素	[✓]	数组 哈希表 分治 5+	🟠	🀄️ 🔗
451	根据字符出现频率排序	[✓]	哈希表 字符串 桶排序 3+	🟠	🀄️ 🔗
973	最接近原点的 K 个点	[✓]	几何 数组 数学 4+	🟠	🀄️ 🔗
1296	划分数组为连续数字的集合		贪心 数组 哈希表 1+	🟠	🀄️ 🔗
239	滑动窗口最大值	[✓]	队列 数组 滑动窗口 2+	🔴	🀄️ 🔗
295	数据流的中位数	[✓]	设计 双指针 数据流 2+	🔴	🀄️ 🔗
23	合并 K 个升序链表	[✓]	链表 分治 堆（优先队列） 1+	🔴	🀄️ 🔗
218	天际线问题		树状数组 线段树 数组 4+	🔴	🀄️ 🔗