463. 岛屿的周长

🟢   🔖  深度优先搜索 广度优先搜索 数组 矩阵  🔗 力扣 LeetCode

题目

You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.

Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).

The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.

Example 1:

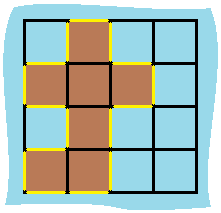
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]

Output: 16

Explanation: The perimeter is the 16 yellow stripes in the image above.

Example 2:

Input: grid = [[1]]

Output: 4

Example 3:

Input: grid = [[1,0]]

Output: 4

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 100
• grid[i][j] is 0 or 1.
• There is exactly one island in grid.

题目大意

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：


输入： grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]

输出： 16

解释： 它的周长是上面图片中的 16 个黄色的边

示例 2：

输入： grid = [[1]]

输出： 4

示例 3：

输入： grid = [[1,0]]

输出： 4

提示：

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 100
• grid[i][j] 为 0 或 1

解题思路

思路一：遍历矩阵

要计算岛屿的周长，可以遍历整个网格，对于每个陆地格子 grid[i][j] == 1，检查其四个相邻方向的格子：

1. 如果相邻的格子是水域或超出网格范围，则当前格子的周长贡献增加 1。
2. 如果相邻的格子是陆地，则不增加贡献。

通过遍历整个网格并按照上述规则计算周长，即可得到最终结果。

1. 初始化 perimeter 变量用于存储周长。
2. 遍历整个网格：
   • 遇到 grid[i][j] == 1 时，检查当前格子的四个方向（上、下、左、右）。
   • 如果某个方向出界或是水域，则 perimeter 加 1。
3. 遍历结束，返回 perimeter。

时间复杂度分析

• 时间复杂度：O(n * m)，其中 n 和 m 分别是网格的行数和列数，因为需要遍历整个网格。
• 空间复杂度：O(1)，除了输入网格，没有使用额外的空间。

---

思路二：深度优先搜索 (DFS)

由于网格中只有单个连通岛屿，所以可以通过 DFS（深度优先搜索） 或 BFS（广度优先搜索） 来遍历岛屿，而不是简单的网格遍历，以减少不必要的网格遍历次数。

1. dfs 函数：

   • 如果当前格子越界或是水域，周长贡献 1。
   • 如果当前格子已访问过（标记为 -1），则不贡献周长，返回 0。
   • 将当前格子标记为已访问。
   • 递归地对四个相邻的格子进行深度优先搜索，将返回的贡献周长累加。

2. 遍历网格：

   • 遍历整个网格，找到第一个陆地格子 grid[i][j] === 1，从该位置开始执行 DFS。
   • 一旦找到一个陆地格子并启动 DFS 之后，就可以提前终止网格遍历，因为题目中只有一个岛屿。
   • 由于岛屿是连通的，DFS 会访问所有的陆地格子，计算出总周长。

复杂度分析

• 时间复杂度：O(n * m)，其中 n 和 m 分别是网格的行数和列数，每个陆地格子最多被访问一次。

• 空间复杂度：O(n)，栈的最大深度为岛屿中的陆地格子数量。

代码

遍历矩阵

/**
 * @param {number[][]} grid
 * @return {number}
 */
var islandPerimeter = function (grid) {
	let perimeter = 0;
	const rows = grid.length;
	const cols = grid[0].length;

	for (let i = 0; i < rows; i++) {
		for (let j = 0; j < cols; j++) {
			if (grid[i][j] === 1) {
				// 上
				if (i === 0 || grid[i - 1][j] === 0) perimeter++;
				// 下
				if (i === rows - 1 || grid[i + 1][j] === 0) perimeter++;
				// 左
				if (j === 0 || grid[i][j - 1] === 0) perimeter++;
				// 右
				if (j === cols - 1 || grid[i][j + 1] === 0) perimeter++;
			}
		}
	}

	return perimeter;
};

深度优先搜索 (DFS)

/**
 * @param {number[][]} grid
 * @return {number}
 */
var islandPerimeter = function (grid) {
	const rows = grid.length;
	const cols = grid[0].length;
	let perimeter = 0;

	// 定义DFS函数
	const dfs = (i, j) => {
		// 边界条件：越界或者遇到水域时，贡献1
		if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] === 0) {
			return 1;
		}
		// 如果已经访问过，直接返回0
		if (grid[i][j] === -1) {
			return 0;
		}

		// 标记为已访问
		grid[i][j] = -1;

		// 递归检查四个方向，并累加周长
		let count = 0;
		count += dfs(i - 1, j); // 上
		count += dfs(i + 1, j); // 下
		count += dfs(i, j - 1); // 左
		count += dfs(i, j + 1); // 右
		return count;
	};

	// 遍历网格，找到第一个陆地开始DFS
	for (let i = 0; i < rows; i++) {
		for (let j = 0; j < cols; j++) {
			if (grid[i][j] === 1) {
				// 执行DFS并返回周长
				return dfs(i, j);
			}
		}
	}

	return 0;
};

相关题目

题号	标题	题解	标签	难度	力扣
695	岛屿的最大面积	[✓]	深度优先搜索 广度优先搜索 并查集 2+	🟠	🀄️ 🔗
733	图像渲染	[✓]	深度优先搜索 广度优先搜索 数组 1+	🟢	🀄️ 🔗
1034	边界着色		深度优先搜索 广度优先搜索 数组 1+	🟠	🀄️ 🔗