407. 接雨水 II

🔴   🔖  广度优先搜索 数组 矩阵 堆（优先队列）  🔗 力扣 LeetCode

题目

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]

Output: 4

Explanation: After the rain, water is trapped between the blocks.

We have two small ponds 1 and 3 units trapped.

The total volume of water trapped is 4.

Example 2:

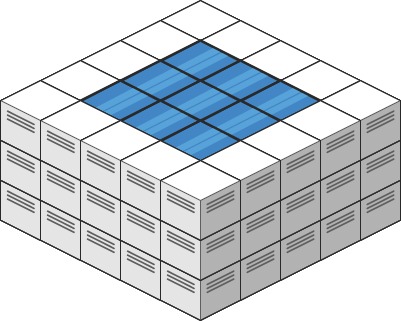
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]

Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 10^4

题目大意

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]

输出: 4

解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为 1+2+1=4。

示例 2:

输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]

输出: 10

提示:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 10^4

解题思路

这道题核心思想是利用最小堆（优先队列）来模拟水位从低向高逐步扩展的过程，逐步计算可储存的水量。

• 每个单元格的储水量由其周围的最低边界决定。储水量取决于该单元格的高度与最低边界高度的差值。
• 如果边界较低，则水会从边界流出，因此边界单元格不储水。

1. 初始化边界

• 矩阵过小（m < 3 或 n < 3）时无法储水，应直接返回 0。
• 使用二维布尔数组 visited 避免重复访问同一单元格。
• 首先将矩阵四周的边界单元格加入最小堆（优先队列），并标记为已访问。
• 边界单元格作为初始水位的最低边界，确保优先处理低高度的单元格，模拟水从低到高扩展的过程。

2. 使用最小堆模拟水位扩展

• 每次从最小堆中取出一个高度最小的单元格，作为当前水位。
• 检查其四个相邻单元格：
  • 如果该相邻单元格未访问，则根据当前单元格的高度计算是否可以储水。
  • 如果可以储水，将储水量累加，并将相邻单元格加入堆中，更新为较高的水位。

3. 更新堆

• 对每个相邻单元格，将其高度更新为两者之间的较大值（模拟水位提升的过程）。
• 将相邻单元格加入最小堆，以便下一次处理更低的单元格。

4. 终止条件

• 当堆为空时，表示所有可以储水的单元格都已处理，返回累积的水量。

复杂度分析

• 时间复杂度：O(m * n * log(m * n))，每个单元格最多访问一次，堆的操作复杂度为 O(log(m * n))。
• 空间复杂度：O(m * n)，最小堆和访问标记数组各占用 O(m * n) 空间。

代码

/**
 * @param {number[][]} heightMap
 * @return {number}
 */
var trapRainWater = function (heightMap) {
	const m = heightMap.length;
	const n = heightMap[0].length;
	if (m < 3 || n < 3) return 0;

	const visited = new Array(m).fill().map(() => new Array(n).fill(false));

	const priority = (a, b) => a[0] < b[0];
	const minHeap = new MinHeap([], priority);

	for (let i = 0; i < m; i++) {
		minHeap.insert([heightMap[i][0], i, 0]);
		minHeap.insert([heightMap[i][n - 1], i, n - 1]);
		visited[i][0] = visited[i][n - 1] = true;
	}

	for (let j = 1; j < n - 1; j++) {
		minHeap.insert([heightMap[0][j], 0, j]);
		minHeap.insert([heightMap[m - 1][j], m - 1, j]);
		visited[0][j] = visited[m - 1][j] = true;
	}

	const dirc = [
		[0, 1],
		[0, -1],
		[1, 0],
		[-1, 0]
	];

	let water = 0;
	while (minHeap.size()) {
		const [height, x, y] = minHeap.pop();
		for (let [dx, dy] of dirc) {
			const nx = x + dx;
			const ny = y + dy;

			if (nx < 0 || nx >= m || ny < 0 || ny >= n || visited[nx][ny]) {
				continue;
			}

			water += Math.max(0, height - heightMap[nx][ny]);
			minHeap.insert([Math.max(height, heightMap[nx][ny]), nx, ny]);
			visited[nx][ny] = true;
		}
	}

	return water;
};

// 最小优先队列
class MinHeap {
	constructor(arr = [], priority = (a, b) => a < b) {
		this.heap = arr;
		this.priority = priority;
		for (let i = Math.floor(this.heap.length / 2) - 1; i >= 0; i--) {
			this.heapifyDown(i);
		}
	}

	insert(num) {
		this.heap.push(num);
		this.heapifyUp(this.heap.length - 1);
	}

	pop() {
		if (this.heap.length === 0) return null;
		const top = this.heap[0];
		const last = this.heap.pop();
		if (this.heap.length > 0) {
			this.heap[0] = last;
			this.heapifyDown(0);
		}
		return top;
	}

	size() {
		return this.heap.length;
	}

	toArray() {
		return this.heap;
	}

	heapifyDown(i) {
		const n = this.heap.length;
		const left = 2 * i + 1;
		const right = 2 * i + 2;
		let smallest = i;

		if (left < n && this.priority(this.heap[left], this.heap[smallest])) {
			smallest = left;
		}
		if (right < n && this.priority(this.heap[right], this.heap[smallest])) {
			smallest = right;
		}

		if (smallest !== i) {
			[this.heap[i], this.heap[smallest]] = [this.heap[smallest], this.heap[i]];
			this.heapifyDown(smallest);
		}
	}

	heapifyUp(i) {
		while (i > 0) {
			const parent = Math.floor((i - 1) / 2);
			if (this.priority(this.heap[i], this.heap[parent])) {
				[this.heap[i], this.heap[parent]] = [this.heap[parent], this.heap[i]];
				i = parent;
			} else {
				break;
			}
		}
	}
}

相关题目

题号	标题	题解	标签	难度	力扣
42	接雨水	[✓]	栈 数组 双指针 2+	🔴	🀄️ 🔗
2503	矩阵查询可获得的最大分数		广度优先搜索 并查集 数组 4+	🔴	🀄️ 🔗