404. 左叶子之和

🟢   🔖  树 深度优先搜索 广度优先搜索 二叉树  🔗 力扣 LeetCode

题目

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1:

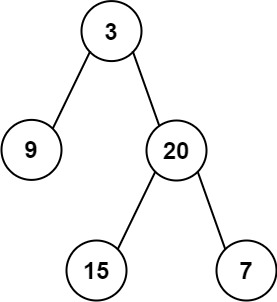
Input: root = [3,9,20,null,null,15,7]

Output: 24

Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1]

Output: 0

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -1000 <= Node.val <= 1000

题目大意

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

输入: root = [3,9,20,null,null,15,7]

输出: 24

解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]

输出: 0

提示:

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

解题思路

思路一：递归

1. 当前节点：
   • 判断其左子节点是否是 左叶子节点。
     • 如果是，则将左子节点的值加入到结果中。
2. 递归向下：
   • 分别对当前节点的左子树和右子树进行递归操作。
3. 返回结果：将所有左叶子节点的值累加并返回。

复杂度分析

• 时间复杂度：O(n)，每个节点遍历一次，n 是树中的节点总数。
• 空间复杂度：O(n)，取决于递归调用栈的深度，最坏情况下是 O(n)（链状树）。

---

思路二：迭代（BFS）

1. 使用队列进行 层序遍历。
2. 遍历过程中：
   • 如果当前节点的左子节点是 左叶子，将其值加入结果中。
   • 将左右子节点继续加入队列，继续遍历。
3. 返回累加的结果。

复杂度分析

• 时间复杂度：O(n)，每个节点遍历一次，n 是树中的节点总数。
• 空间复杂度：O(n)，取决于队列的最大长度，最坏情况下是 O(n)。

代码

递归

/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumOfLeftLeaves = function (root) {
	if (!root) return 0;

	let sum = 0;

	// 判断左子节点是否是左叶子节点
	if (root.left && !root.left.left && !root.left.right) {
		sum += root.left.val;
	}

	// 递归左右子树
	sum += sumOfLeftLeaves(root.left);
	sum += sumOfLeftLeaves(root.right);

	return sum;
};

迭代（BFS）

/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumOfLeftLeaves = function (root) {
	if (!root) return 0;

	let sum = 0;
	let queue = [root];

	while (queue.length > 0) {
		let node = queue.shift();

		// 检查左子节点是否是左叶子
		if (node.left && !node.left.left && !node.left.right) {
			sum += node.left.val;
		}

		// 继续遍历左右子树
		if (node.left) queue.push(node.left);
		if (node.right) queue.push(node.right);
	}

	return sum;
};