452. 用最少数量的箭引爆气球

🟠   🔖  贪心 数组 排序  🔗 力扣 LeetCode

题目

There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.

Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.

Given the array points, return the minimum number of arrows that must be shot to burst all balloons.

Example 1:

Input: points = [[10,16],[2,8],[1,6],[7,12]]

Output: 2

Explanation: The balloons can be burst by 2 arrows:

• Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6].
• Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].

Example 2:

Input: points = [[1,2],[3,4],[5,6],[7,8]]

Output: 4

Explanation: One arrow needs to be shot for each balloon for a total of 4 arrows.

Example 3:

Input: points = [[1,2],[2,3],[3,4],[4,5]]

Output: 2

Explanation: The balloons can be burst by 2 arrows:

• Shoot an arrow at x = 2, bursting the balloons [1,2] and [2,3].
• Shoot an arrow at x = 4, bursting the balloons [3,4] and [4,5].

Constraints:

• 1 <= points.length <= 10^5
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

题目大意

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中 points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend 之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1:

输入: points = [[10,16],[2,8],[1,6],[7,12]]

输出: 2

解释：气球可以用 2 支箭来爆破:

• 在 x = 6 处射出箭，击破气球[2,8]和[1,6]。
• 在 x = 11 处发射箭，击破气球[10,16]和[7,12]。

示例 2:

输入: points = [[1,2],[3,4],[5,6],[7,8]]

输出: 4

解释：每个气球需要射出一支箭，总共需要 4 支箭。

示例 3:

输入: points = [[1,2],[2,3],[3,4],[4,5]]

输出: 2

解释：气球可以用 2 支箭来爆破:

• 在 x = 2 处发射箭，击破气球[1,2]和[2,3]。
• 在 x = 4 处射出箭，击破气球[3,4]和[4,5]。

解题思路

1. 按照区间的起点进行升序排序，若起点相同时按照区间的终点进行降序排列；
2. 两个相邻区间可能有如下三种情况：

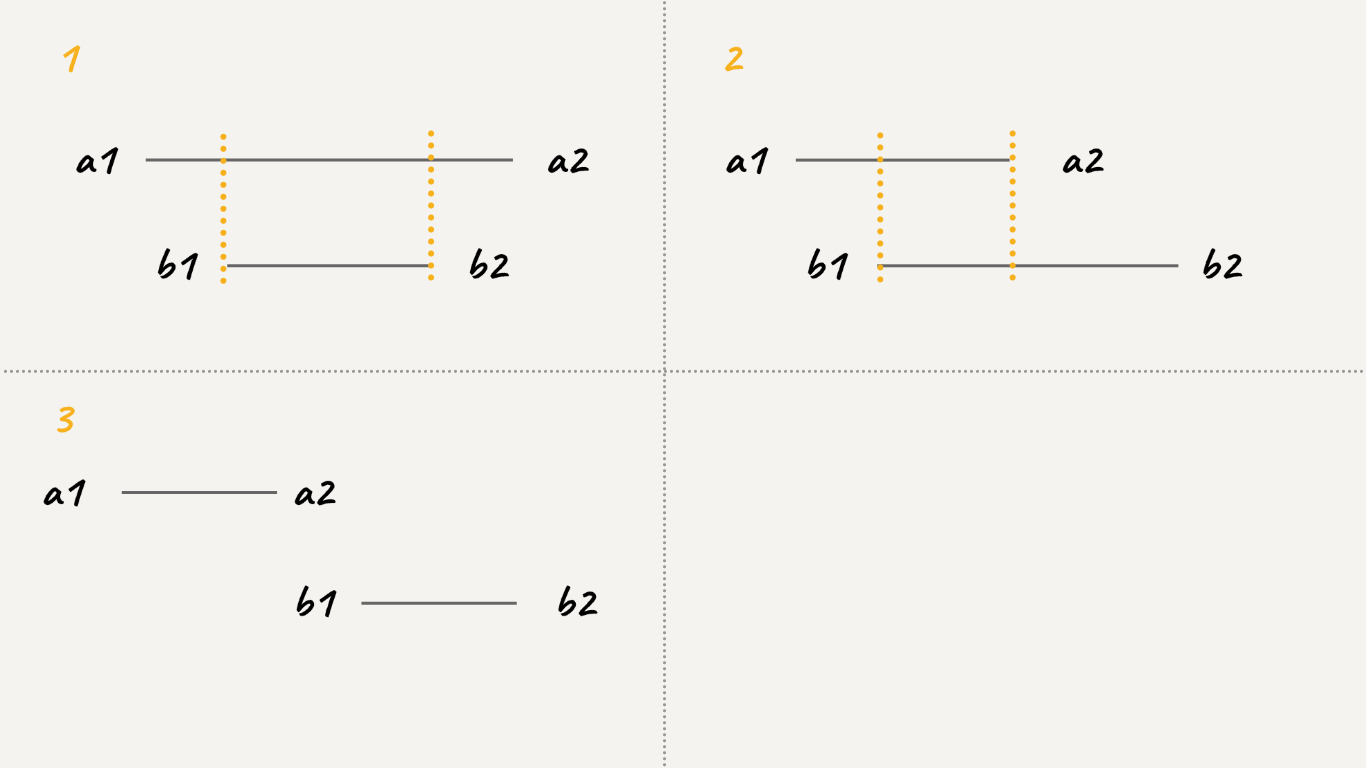
3. 起点升序排序之后，一定有 a1 <= b1，所以只需要对比和更新终点的情况：

• 对于情况一，找到了重合区间 [b1, b2]，可共用弓箭数加一，继续比较后续区间是否和 [b1, b2] 重合，所以更新终点为 b2；
• 对于情况二，找到了重合区间 [b1, a2]，可共用弓箭数加一，继续比较后续区间是否和 [b1, a2] 重合，终点依然为 a2；
• 对于情况三，两个区间完全不重合，更新终点终点为 b2；

4. 最后返回总区间数减去可共用弓箭数 points.length - count；

代码

/**
 * @param {number[][]} points
 * @return {number}
 */
var findMinArrowShots = function (points) {
	// 按照起点升序排列，起点相同时，按终点降序排列
	points.sort((a, b) => {
		if (a[0] == [b[0]]) {
			return b[1] - a[1];
		}
		return a[0] - b[0];
	});

	// 记录可共用弓箭的数量
	let count = 0;
	// 记录重合区间的起点和终点
	let [a1, a2] = points[0];

	for (let i = 1; i < points.length; i++) {
		const [b1, b2] = points[i];
		// 情况一，找到重合区间，更新终点为重合区间的终点 b2
		if (a2 > b2) {
			count++;
			a2 = b2;
		}
		// 情况二，找到重合区间，重合区间的终点就是 a2，不用更新
		else if (a2 >= b1 && a2 <= b2) {
			count++;
		}
		// 情况三，俩区间不重合，更新终点为 b2
		else {
			a2 = b2;
		}
	}
	return points.length - count;
};

相关题目

题号	标题	题解	标签	难度	力扣
253	会议室 II 🔒		贪心 数组 双指针 3+	🟠	🀄️ 🔗
435	无重叠区间	[✓]	贪心 数组 动态规划 1+	🟠	🀄️ 🔗