441. 排列硬币

🟢   🔖  数学 二分查找  🔗 力扣 LeetCode

题目

You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number ofcomplete rows of the staircase you will build.

Example 1:

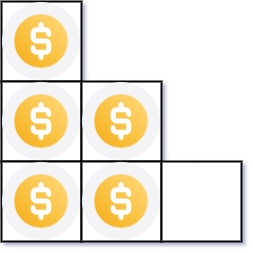
Input: n = 5

Output: 2

Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

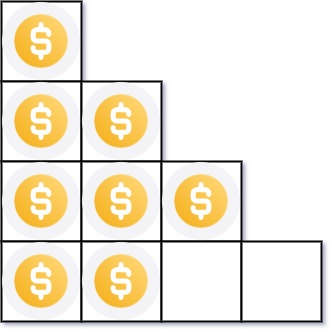
Input: n = 8

Output: 3

Explanation: Because the 4th row is incomplete, we return 3.

Constraints:

• 1 <= n <= 231 - 1

题目大意

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i ** 行必须正好有 i ** 枚硬币。阶梯的最后一行 可能 是不完整的。

给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

示例 1：

输入： n = 5

输出： 2

解释： 因为第三行不完整，所以返回 2 。

示例 2：

输入： n = 8

输出： 3

解释： 因为第四行不完整，所以返回 3 。

提示：

• 1 <= n <= 231 - 1

解题思路

这道题的本质是寻找一个最大的整数 k，满足阶梯总硬币数公式：(k * (k + 1)) / 2 <= n，即找到 k 使得从第 1 行到第 k 行的硬币总数小于等于 n。

因为阶梯行数 k 和硬币总数 n 的关系是单调递增的，使用 二分查找 是一个高效的解决方法。

1. 初始化 left = 1 和 right = n，定义搜索范围。
2. 在二分查找的过程中，计算中点 mid，检查是否满足公式 (mid * (mid + 1)) / 2 <= n。
3. 根据公式的结果调整搜索范围：
   • 如果超出硬币总数，减小搜索范围，调整 right = mid - 1。
   • 如果可以满足，则记录结果，并尝试扩大范围 left = mid + 1。
4. 当循环结束时，res 保存的就是可以构成完整阶梯行的最大行数，返回记录的最大行数 res。

复杂度分析

• 时间复杂度：O(log n)，每次二分查找将范围缩小一半，总共进行 O(log n) 次计算。
• 空间复杂度：O(1)，只使用了常数个变量。

代码

/**
 * @param {number} n
 * @return {number}
 */
var arrangeCoins = function (n) {
	let left = 1,
		right = n,
		res = 0; // 初始化搜索范围和结果
	while (left <= right) {
		const mid = Math.floor((left + right) / 2); // 计算中间值
		const total = (mid * (mid + 1)) / 2; // 计算当前阶梯的硬币总数
		if (total > n) {
			right = mid - 1; // 超出硬币总数，缩小范围
		} else {
			res = mid; // 记录当前结果
			left = mid + 1; // 尝试检查更大的阶梯行数
		}
	}
	return res; // 返回最终结果
};