331. 验证二叉树的前序序列化
331. 验证二叉树的前序序列化
题目
One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node's value. If it is a null node, we record using a sentinel value such as '#'.
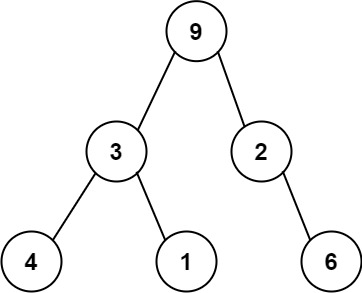
For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.
Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.
It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.
You may assume that the input format is always valid.
- For example, it could never contain two consecutive commas, such as
"1,,3".
**Note: **You are not allowed to reconstruct the tree.
Example 1:
Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output: true
Example 2:
Input: preorder = "1,#"
Output: false
Example 3:
Input: preorder = "9,#,#,1"
Output: false
Constraints:
1 <= preorder.length <= 10^4preorderconsist of integers in the range[0, 100]and'#'separated by commas','.
题目大意
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。

例如,上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#",其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
你可以认为输入格式总是有效的
- 例如它永远不会包含两个连续的逗号,比如
"1,,3"。
注意: 不允许重建树。
示例 1:
输入: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
**输出:**true
示例 2:
输入: preorder = "1,#"
**输出:**false
示例 3:
输入: preorder = "9,#,#,1"
**输出:**false
提示:
1 <= preorder.length <= 10^4preorder由以逗号“,”分隔的[0,100]范围内的整数和“#”组成
解题思路
使用一个指针
i遍历preorder,初始指向根节点。DFS 验证序列化,定义递归函数
dfs()来验证子树是否合法:- 如果当前节点是
#,直接返回true(空节点合法)。 - 如果是非空节点,则递归检查左子树和右子树。
- 如果当前节点是
最终需要检查:
dfs()是否成功完成。- 遍历的节点数是否恰好覆盖了
preorder。
非法情况:
- 空节点数量不足,遍历时
i超出数组长度。 - 子树验证完成后,仍有未使用的节点(即多余的节点)。
- 空节点数量不足,遍历时
复杂度分析
- 时间复杂度:
O(n),其中n是preorder的长度,每个节点最多访问一次。 - 空间复杂度:
O(h),其中h是树的高度,递归调用栈的空间复杂度为O(h),最差情况下为O(n)。
代码
/**
* @param {string} preorder
* @return {boolean}
*/
var isValidSerialization = function (preorder) {
const nodes = preorder.split(',');
let i = 0;
const dfs = () => {
if (i >= nodes.length) return false; // 越界情况
if (nodes[i++] === '#') return true; // 空节点,合法
return dfs() && dfs(); // 递归验证左、右子树
};
return dfs() && i === nodes.length; // 检查是否完整遍历
};
