304. 二维区域和检索 - 矩阵不可变

🟠   🔖  设计 数组 矩阵 前缀和  🔗 力扣 LeetCode

题目

Given a 2D matrix matrix, handle multiple queries of the following type:

• Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

• NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
• int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

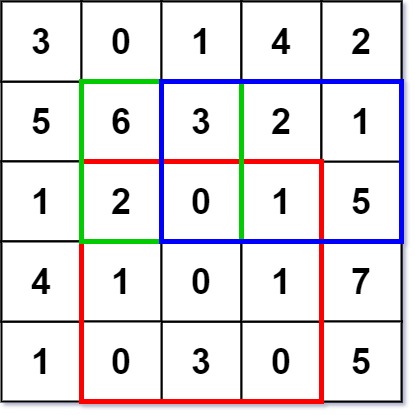
Input

["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]

[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

Output

[null, 8, 11, 12]

Explanation

NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);

numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)

numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)

numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10^4 <= matrix[i][j] <= 10^4
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• At most 10^4 calls will be made to sumRegion.

题目大意

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

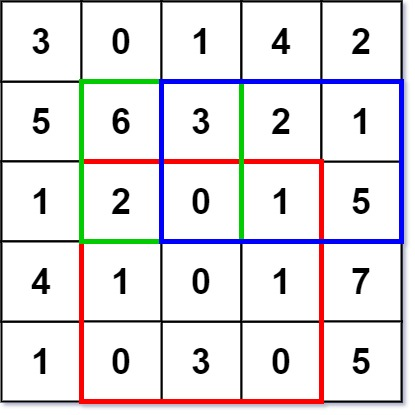
输入:

["NumMatrix","sumRegion","sumRegion","sumRegion"]

[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]

输出:

[null, 8, 11, 12]

解释:

NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);

numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)

numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)

numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10^5 <= matrix[i][j] <= 10^5
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 10^4 次 sumRegion 方法

解题思路

1. 构建前缀和数组：

   • 使用一个二维数组 sum 存储前缀和。
   • sum[i][j] 表示从左上角 (0, 0) 到当前位置 (i-1, j-1) 的子矩阵元素总和。
   • sum[i][j] 的递推公式为：

     sum[i][j] = matrix[i-1][j-1] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]
     

     其中：
     • matrix[i-1][j-1] 是当前元素。
     • sum[i-1][j] 是上一行累积的前缀和。
     • sum[i][j-1] 是当前行左边累积的前缀和。
     • sum[i-1][j-1] 是重复计算的区域，需要减掉。

2. 查询区域和：

   • 对于任意给定的矩阵区域 (row1, col1) 到 (row2, col2)，区域和可以通过前缀和数组快速计算：

     sumRegion = sum[row2+1][col2+1]
               - sum[row1][col2+1]
               - sum[row2+1][col1]
               + sum[row1][col1]
     

     其中：
     • sum[row2+1][col2+1] 是完整区域的前缀和。
     • sum[row1][col2+1] 是去掉上方区域的前缀和。
     • sum[row2+1][col1] 是去掉左侧区域的前缀和。
     • sum[row1][col1] 是上方和左侧重叠区域的前缀和，需要加回来。

复杂度分析

• 时间复杂度：
  • 构造：计算前缀和需要遍历整个矩阵，时间复杂度为 O(m * n)，其中 m 是矩阵的行数，n 是矩阵的列数。
  • 查询：每次查询只涉及常数次加减法操作，因此时间复杂度为 O(1)。
• 空间复杂度：O(m * n)，需要一个大小为 (m + 1) x (n + 1) 的二维数组存储前缀和。

代码

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function (matrix) {
	const m = matrix.length;
	const n = matrix[0].length;
	this.sum = new Array(m + 1).fill().map(() => new Array(n + 1).fill(0));

	for (let i = 1; i <= m; i++) {
		for (let j = 1; j <= n; j++) {
			this.sum[i][j] =
				matrix[i - 1][j - 1] +
				this.sum[i - 1][j] +
				this.sum[i][j - 1] -
				this.sum[i - 1][j - 1];
		}
	}
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function (row1, col1, row2, col2) {
	return (
		this.sum[row2 + 1][col2 + 1] -
		this.sum[row1][col2 + 1] -
		this.sum[row2 + 1][col1] +
		this.sum[row1][col1]
	);
};

相关题目

题号	标题	题解	标签	难度	力扣
303	区域和检索 - 数组不可变	[✓]	设计 数组 前缀和	🟢	🀄️ 🔗
308	二维区域和检索 - 矩阵可修改 🔒		设计 树状数组 线段树 2+	🔴	🀄️ 🔗
3030	找出网格的区域平均强度		数组 矩阵	🟠	🀄️ 🔗