310. 最小高度树

🟠   🔖  深度优先搜索 广度优先搜索 图 拓扑排序  🔗 力扣 LeetCode

题目

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of allMHTs ' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]

Output: [1]

Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

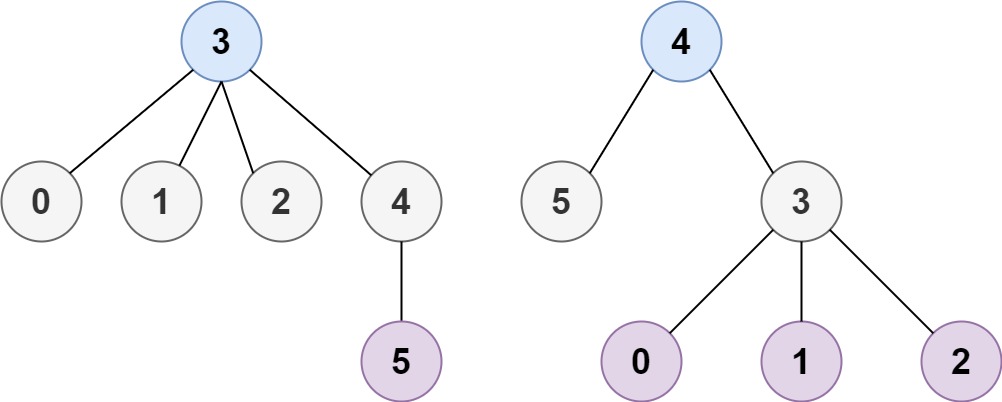
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]

Output: [3,4]

Constraints:

• 1 <= n <= 2 * 10^4
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

题目大意

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，任何一个没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

输入： n = 4, edges = [[1,0],[1,2],[1,3]]

输出：[1]

解释： 如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

输入： n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]

输出：[3,4]

提示：

• 1 <= n <= 2 * 10^4
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• 所有 (ai, bi) 互不相同
• 给定的输入 保证 是一棵树，并且 不会有重复的边

解题思路

1. 树的直径特性：

   • 最小高度树的根节点一定是树的直径的中点。
   • 树的直径是指树中任意两个节点之间最长路径的长度。树的直径的中点（1 个或 2 个）就是最小高度树的根节点。
   • 可以通过逐层移除叶节点的方法，找到树的直径的中点。

2. 构造图：

   • 用邻接表表示树的结构。

3. 找到所有叶节点：

   • 叶节点是指度为 1 的节点。

4. 逐层移除叶节点：

   • 每次将当前所有叶节点移除，同时更新与这些叶节点相连的节点的度数。
   • 如果某个节点的度数变为 1，它成为新的叶节点。

5. 终止条件：

   • 当剩余节点数小于或等于 2 时，停止移除。这些剩余的节点就是树的直径的中点，也就是最小高度树的根节点。

复杂度分析

• 时间复杂度：O(n)，构建图的时间复杂度为 O(n)，逐层移除叶节点的复杂度也为 O(n)，总体时间复杂度为 O(n)。
• 空间复杂度：O(n)，邻接表的空间复杂度为 O(n)，队列的空间复杂度为 O(n)，总体为 O(n)。

代码

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findMinHeightTrees = function (n, edges) {
	if (n === 1) return [0]; // 特殊情况：只有一个节点
	if (n === 2) return [0, 1]; // 特殊情况：两个节点

	// 构建邻接表
	const graph = new Array(n).fill(0).map(() => []);
	for (const [u, v] of edges) {
		graph[u].push(v);
		graph[v].push(u);
	}

	// 找到所有叶节点（度为 1 的节点）
	const leaves = [];
	const degree = new Array(n).fill(0);
	for (let i = 0; i < n; i++) {
		degree[i] = graph[i].length;
		if (degree[i] === 1) leaves.push(i);
	}

	// 逐层移除叶节点
	let remainingNodes = n;
	while (remainingNodes > 2) {
		const size = leaves.length;
		remainingNodes -= size;

		for (let i = 0; i < size; i++) {
			const leaf = leaves.shift();
			for (const neighbor of graph[leaf]) {
				degree[neighbor]--;
				if (degree[neighbor] === 1) leaves.push(neighbor);
			}
		}
	}

	// 剩余节点即为结果
	return leaves;
};

相关题目

题号	标题	题解	标签	难度	力扣
207	课程表	[✓]	深度优先搜索 广度优先搜索 图 1+	🟠	🀄️ 🔗
210	课程表 II	[✓]	深度优先搜索 广度优先搜索 图 1+	🟠	🀄️ 🔗
2603	收集树中金币		树 图 拓扑排序 1+	🔴	🀄️ 🔗
3067	在带权树网络中统计可连接服务器对数目		树 深度优先搜索 数组	🟠	🀄️ 🔗
3203	合并两棵树后的最小直径	[✓]	树 深度优先搜索 广度优先搜索 1+	🔴	🀄️ 🔗