319. 灯泡开关

🟠   🔖  脑筋急转弯 数学  🔗 力扣 LeetCode

题目

There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.

On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.

Return the number of bulbs that are on aftern rounds.

Example 1:

Input: n = 3

Output: 1

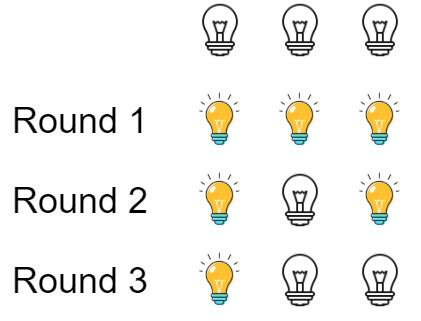
Explanation: At first, the three bulbs are [off, off, off].

After the first round, the three bulbs are [on, on, on].

After the second round, the three bulbs are [on, off, on].

After the third round, the three bulbs are [on, off, off].

So you should return 1 because there is only one bulb is on.

Example 2:

Input: n = 0

Output: 0

Example 3:

Input: n = 1

Output: 1

Constraints:

• 0 <= n <= 10^9

题目大意

初始时有 n 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭第二个。

第三轮，你每三个灯泡就切换第三个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i 个灯泡就切换第 i 个灯泡的开关。直到第 n 轮，你只需要切换最后一个灯泡的开关。

找出并返回 n 轮后有多少个亮着的灯泡。

示例 1：

输入： n = 3

输出： 1

解释：

初始时, 灯泡状态 [关闭, 关闭, 关闭].

第一轮后, 灯泡状态 [开启, 开启, 开启].

第二轮后, 灯泡状态 [开启, 关闭, 开启].

第三轮后, 灯泡状态 [开启, 关闭, 关闭].

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

输入： n = 0

输出： 0

示例 3：

输入： n = 1

输出： 1

提示：

• 0 <= n <= 10^9

解题思路

1. 状态变化规律

• 灯泡是否亮着，取决于它被切换的次数：
  • 如果一个灯泡的编号有奇数个因数，则它是亮的。
  • 如果一个灯泡的编号有偶数个因数，则它是灭的。

2. 数学分析

• 一个数的因数通常是成对出现的，例如：
  • 6 的因数有 {1, 6}, {2, 3}，因数成对。
• 只有 完全平方数 才有奇数个因数，例如：
  • 9 的因数有 {1, 9}, {3}，因数不成对。

3. 问题转化

• 问题变为：n 的范围内有多少个完全平方数。
  • 这等价于求 floor(sqrt(n))，即平方数的个数。

复杂度分析

• 时间复杂度：O(1)，计算平方根的时间复杂度为 O(1)。
• 空间复杂度：O(1)，只需常数额外空间。

代码

/**
 * @param {number} n
 * @return {number}
 */
var bulbSwitch = function (n) {
	return Math.floor(Math.sqrt(n));
};

相关题目

题号	标题	题解	标签	难度	力扣
672	灯泡开关 Ⅱ		位运算 深度优先搜索 广度优先搜索 1+	🟠	🀄️ 🔗
995	K 连续位的最小翻转次数		位运算 队列 数组 2+	🔴	🀄️ 🔗
1375	二进制字符串前缀一致的次数		数组	🟠	🀄️ 🔗
2485	找出中枢整数		数学 前缀和	🟢	🀄️ 🔗