212. 单词搜索 II

🔴   🔖  字典树 数组 字符串 回溯 矩阵  🔗 力扣 LeetCode

题目

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]

Output: ["eat","oath"]

Example 2:

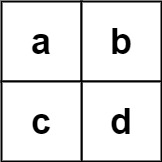
Input: board = [["a","b"],["c","d"]], words = ["abcb"]

Output: []

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 10^4
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

题目大意

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words， 返回所有二维网格上的单词 。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

解题思路

• 这是一个二维网格中的路径搜索问题，需要找到符合条件的单词。和普通的 DFS（深度优先搜索）不同，这里有多个目标单词，直接对每个单词进行搜索可能效率较低。
• 利用**字典树（Trie）**可以高效处理多个单词的匹配问题。我们可以将所有单词构建成字典树，然后使用 DFS 在网格中搜索可能的路径，并利用字典树加速单词匹配过程。

1. 构建字典树：

   • 使用 buildTrie 函数构建一个字典树，将单词列表中的每个单词插入到字典树中。
   • 每个字母对应一个字典树节点，最终将完整的单词存储在叶子节点的 word 属性中。

2. DFS 搜索：

   • 在 findWords 函数中，遍历网格的每个单元格，启动 DFS 搜索。
   • 使用 DFS 搜索过程中，如果找到字典树中的单词，将其添加到结果列表 res 中。
   • 通过设置 board[r][c] = '#' 标记访问过的单元格，避免回溯时重复访问。搜索结束后再恢复原始字母。

3. 剪枝和优化：

   • 如果当前节点的字母不在字典树的子节点中（node[board[r][c]] 为 null），可以立即返回。
   • 当找到完整单词后，将其从字典树中移除（node.word = null），防止重复添加相同单词。

4. 恢复网格状态：

   • 在递归搜索结束后，恢复当前单元格的字母，继续其他方向的搜索。

复杂度分析

• 时间复杂度：

  • 构建字典树：O(L)，其中 L 是所有单词的字符总数。
  • DFS 搜索：在最坏情况下，每个单元格都会访问一次，每次可能最多探索四个方向，时间复杂度为 O(m * n * 4^k)，其中 m 和 n 是网格的行数和列数，k 是最长单词的长度。

• 空间复杂度：

  • 字典树占用的空间为 O(L)，递归调用的栈深度为 O(k)，其中 L 是单词总字符数，k 是单词的最大长度。

代码

/**
 * @param {character[][]} board
 * @param {string[]} words
 * @return {string[]}
 */
var findWords = function (board, words) {
	let res = [],
		root = buildTrie(words);

	const rows = board.length,
		cols = board[0].length;

	// DFS 搜索
	const dfs = (node, r, c) => {
		if (r < 0 || r >= rows || c < 0 || c >= cols || !node[board[r][c]]) {
			return;
		}
		const char = board[r][c];
		const nextNode = node[char];
		if (nextNode.word) {
			res.push(nextNode.word);
			// 防止重复找到相同的单词
			nextNode.word = null;
		}

		// 标记访问过的单元格
		board[r][c] = '#';

		// 搜索四个方向
		dfs(nextNode, r - 1, c); // 上
		dfs(nextNode, r + 1, c); // 下
		dfs(nextNode, r, c - 1); // 左
		dfs(nextNode, r, c + 1); // 右

		// 恢复当前单元格的值
		board[r][c] = char;
	};

	// 遍历网格的每个位置，启动DFS搜索
	for (let r = 0; r < rows; r++) {
		for (let c = 0; c < cols; c++) {
			dfs(root, r, c);
		}
	}

	return res;
};

// 构建字典树
var buildTrie = function (words) {
	const root = {};
	for (let word of words) {
		let node = root;
		for (let char of word) {
			if (!node[char]) {
				node[char] = {};
			}
			node = node[char];
		}
		// 在叶子节点存储完整的单词
		node.word = word;
	}
	return root;
};

相关题目

题号	标题	题解	标签	难度	力扣
79	单词搜索	[✓]	数组 字符串 回溯 1+	🟠	🀄️ 🔗
980	不同路径 III		位运算 数组 回溯 1+	🔴	🀄️ 🔗
2227	加密解密字符串		设计 字典树 数组 2+	🔴	🀄️ 🔗