598. 区间加法 II
598. 区间加法 II
题目
You are given an m x n matrix M initialized with all 0's and an array of operations ops, where ops[i] = [ai, bi] means M[x][y] should be incremented by one for all 0 <= x < ai and 0 <= y < bi.
Count and return the number of maximum integers in the matrix after performing all the operations.
Example 1:
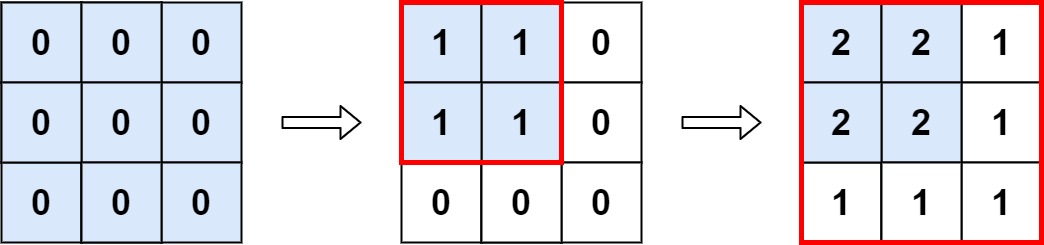
Input: m = 3, n = 3, ops = [[2,2],[3,3]]
Output: 4
Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.
Example 2:
Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
Output: 4
Example 3:
Input: m = 3, n = 3, ops = []
Output: 9
Constraints:
1 <= m, n <= 4 * 10^40 <= ops.length <= 10^4ops[i].length == 21 <= ai <= m1 <= bi <= n
题目大意
给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时, M[x][y] 应该加 1。
在 执行完所有操作后 ,计算并返回 矩阵中最大整数的个数 。
示例 1:

输入: m = 3, n = 3,ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有 4 个值为 2 的元素。因此返回 4。
示例 2:
输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4
示例 3:
输入: m = 3, n = 3, ops = []
输出: 9
提示:
1 <= m, n <= 4 * 10^40 <= ops.length <= 10^4ops[i].length == 21 <= ai <= m1 <= bi <= n
解题思路
值最大的区域
- 对于每次操作
ops[i] = [a, b],会对矩形(0,0)到(a-1, b-1)的区域加 1。 - 因此,值最大的区域会被所有操作重叠,实际是所有操作中矩形的最小范围交集。
- 对于每次操作
如何计算最小范围交集
- 遍历
ops数组,对a和b分别取最小值,得到操作后的最小行minRow和最小列minCol。 - 矩形网格的最大值区域即为大小为
minRow × minCol的矩形区域。
- 遍历
特殊情况
- 如果
ops是空数组,没有任何操作,值最大的网格区域就是整个矩形m × n。
- 如果
复杂度分析
- 时间复杂度:
O(k),其中k是ops的长度,遍历ops一次。 - 空间复杂度:
O(1),只使用了常量空间。
代码
/**
* @param {number} m
* @param {number} n
* @param {number[][]} ops
* @return {number}
*/
var maxCount = function (m, n, ops) {
let minRow = m; // 初始为矩阵行数
let minCol = n; // 初始为矩阵列数
// 遍历操作,计算最小行数和列数
for (let [a, b] of ops) {
minRow = Math.min(minRow, a);
minCol = Math.min(minCol, b);
}
// 最大值区域的网格数量
return minRow * minCol;
};
相关题目
| 题号 | 标题 | 题解 | 标签 | 难度 | 力扣 |
|---|---|---|---|---|---|
| 370 | 区间加法 🔒 | 数组 前缀和 | 🟠 | 🀄️ 🔗 | |
| 2718 | 查询后矩阵的和 | 数组 哈希表 | 🟠 | 🀄️ 🔗 |
