566. 重塑矩阵

🟢 🔖 数组 矩阵 模拟 🔗 力扣open in new window LeetCodeopen in new window

题目

In MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.

You are given an m x n matrix mat and two integers r and c representing the number of rows and the number of columns of the wanted reshaped matrix.

The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.

If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.

Example 1:

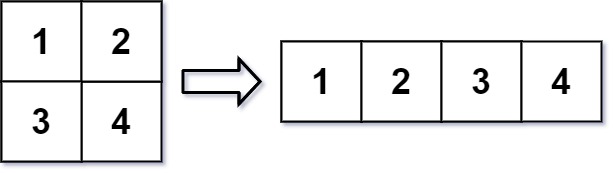
Input: mat = [[1,2],[3,4]], r = 1, c = 4
Output: [[1,2,3,4]]

Example 2:

Input: mat = [[1,2],[3,4]], r = 2, c = 4
Output: [[1,2],[3,4]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 100
-1000 <= mat[i][j] <= 1000
1 <= r, c <= 300

题目大意

在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。

给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序 填充。

如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

示例 1：

输入： mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]

示例 2：

输入： mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 100
-1000 <= mat[i][j] <= 1000
1 <= r, c <= 300

解题思路

获取矩阵尺寸
- m 和 n 分别表示原矩阵的行数和列数。
- 检查原矩阵的元素总数 m * n 是否等于新矩阵的元素总数 r * c。如果不等，直接返回原矩阵。
计算索引映射
- 将二维索引映射到一维索引：
  - 原矩阵的元素 mat[i][j] 的一维索引为 idx = i * n + j。
- 一维索引映射到新矩阵的二维索引：
  - 新矩阵的行号为 i = Math.floor(idx / c)。
  - 新矩阵的列号为 j = idx % c。
构建结果矩阵
- 使用嵌套循环遍历新矩阵的每个元素，根据上述公式计算其对应的原矩阵元素，并填充到新矩阵。
返回结果
- 返回构造的结果矩阵 res。

复杂度分析

时间复杂度：O(m * n)，遍历矩阵中的所有元素。
空间复杂度：O(r * c)，构造了一个新矩阵。

代码

/**
 * @param {number[][]} mat
 * @param {number} r
 * @param {number} c
 * @return {number[][]}
 */
var matrixReshape = function (mat, r, c) {
	// 获取原矩阵行数和列数
	const m = mat.length,
		n = mat[0].length;

	// 如果元素总数不同，直接返回原矩阵
	if (m * n !== r * c) return mat;

	// 初始化新矩阵
	let res = new Array(r).fill().map(() => new Array(c));

	// 遍历新矩阵，按照索引映射填充元素
	for (let i = 0; i < r; i++) {
		for (let j = 0; j < c; j++) {
			const idx = i * c + j; // 一维索引
			res[i][j] = mat[Math.floor(idx / n)][idx % n]; // 映射到原矩阵
		}
	}
	return res; // 返回新矩阵
};

566. 重塑矩阵

# 566. 重塑矩阵

# 题目

# 题目大意

# 解题思路

# 复杂度分析

# 代码

# 相关题目

566. 重塑矩阵

题目

题目大意

解题思路

复杂度分析

代码

相关题目