516. 最长回文子序列

🟠   🔖  字符串 动态规划  🔗 力扣 LeetCode

题目

Given a string s, find the longest palindromic subsequence 's length in s.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1:

Input: s = "bbbab"

Output: 4

Explanation: One possible longest palindromic subsequence is "bbbb".

Example 2:

Input: s = "cbbd"

Output: 2

Explanation: One possible longest palindromic subsequence is "bb".

Constraints:

• 1 <= s.length <= 1000
• s consists only of lowercase English letters.

题目大意

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

s 仅由小写英文字母组成。

解题思路

这个问题可以使用动态规划来解决。们定义一个二维数组 dp，其中 dp[i][j] 表示字符串 s 在区间 [i, j] 内的最长回文子序列的长度。使用动态规划的方法来填充这个二维数组。

1. 初始化动态规划数组： 对角线上的元素 dp[i][i] 均为 1，因为任何一个单个字符都是回文子序列。

2. 状态转移：

   • 当 s[i] === s[j] 时，表示两个字符相同，可以将两个字符加入到已经找到的回文子序列中，因此 dp[i][j] = dp[i+1][j-1] + 2。
   • 当 s[i] !== s[j] 时，表示两个字符不同，我们需要考虑去掉其中一个字符，然后取另一个区间的最长回文子序列，即 dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1])。

3. 遍历顺序： 由于状态转移方程需要依赖区间 [i+1, j-1], [i+1, j], [i, j-1] 的结果，因此我们需要按照区间长度从小到大的顺序遍历区间，即先遍历较短的区间，再根据较短区间的结果计算较长区间的结果。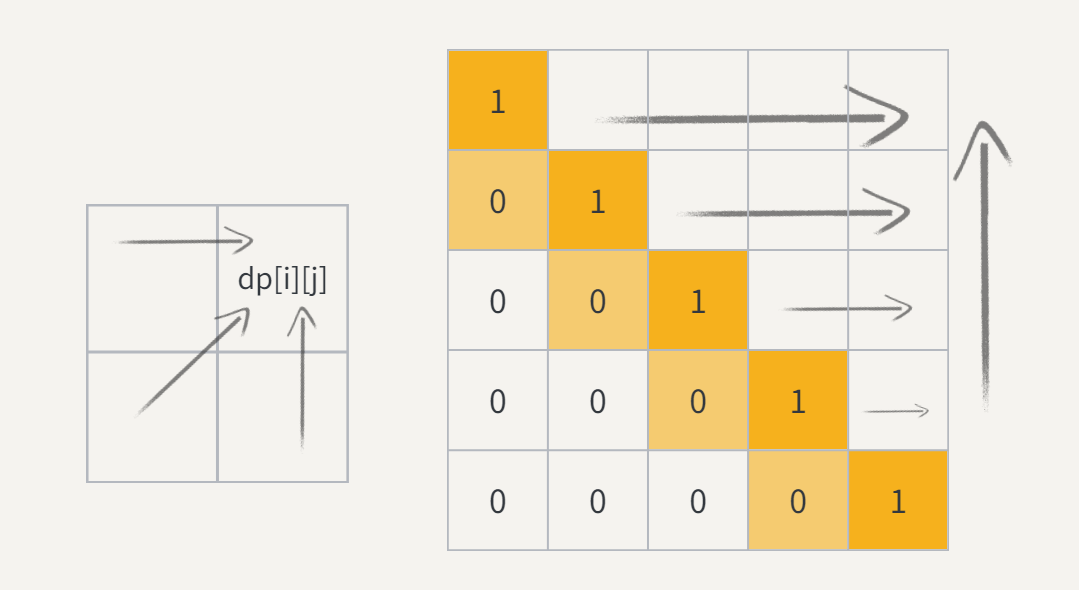

   

4. 返回结果： 最终结果存储在 dp[0][n-1] 中，即整个字符串的最长回文子序列长度。

复杂度分析

• 时间复杂度：O(n^2)，其中 n 是字符串的长度，动态规划数组的大小为 n^2。
• 空间复杂度：O(n^2)，使用了一个二维动态规划数组。

代码

/**
 * @param {string} s
 * @return {number}
 */
var longestPalindromeSubseq = function (s) {
	const n = s.length;
	let dp = new Array(n).fill(0).map((i) => new Array(n).fill(0));

	// 初始化动态规划数组
	for (let i = 0; i < n; i++) {
		dp[i][i] = 1;
	}

	// 遍历区间长度
	for (let i = n - 2; i >= 0; i--) {
		for (let j = i + 1; j < n; j++) {
			if (s[i] == s[j]) {
				dp[i][j] = dp[i + 1][j - 1] + 2;
			} else {
				dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
			}
		}
	}
	return dp[0][n - 1];
};

相关题目

题号	标题	题解	标签	难度	力扣
5	最长回文子串	[✓]	双指针 字符串 动态规划	🟠	🀄️ 🔗
647	回文子串		双指针 字符串 动态规划	🟠	🀄️ 🔗
730	统计不同回文子序列		字符串 动态规划	🔴	🀄️ 🔗
1143	最长公共子序列	[✓]	字符串 动态规划	🟠	🀄️ 🔗
1682	最长回文子序列 II 🔒		字符串 动态规划	🟠	🀄️ 🔗
1771	由子序列构造的最长回文串的长度		字符串 动态规划	🔴	🀄️ 🔗
2002	两个回文子序列长度的最大乘积		位运算 字符串 动态规划 2+	🟠	🀄️ 🔗