542. 01 矩阵

🟠   🔖  广度优先搜索 数组 动态规划 矩阵  🔗 力扣 LeetCode

题目

Given an m x n binary matrix mat, return the distance of the nearest0for each cell.

The distance between two adjacent cells is 1.

Example 1:

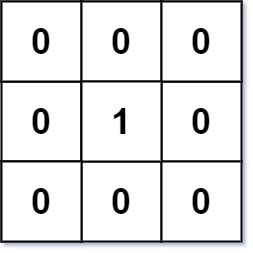
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]

Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

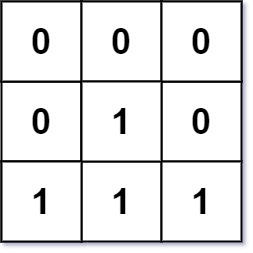
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]

Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

题目大意

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

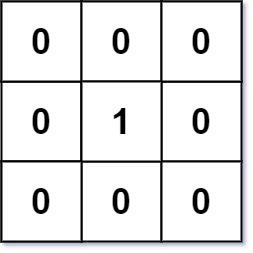
输入： mat = [[0,0,0],[0,1,0],[0,0,0]]

输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

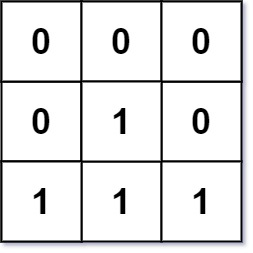
输入： mat = [[0,0,0],[0,1,0],[1,1,1]]

输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

解题思路

题目要求计算每个 1 到最近的 0 的最短距离。由于 1 只能通过 4 个方向（上、下、左、右）移动，这类 最短路径问题 适合使用 BFS（广度优先搜索） 进行求解，由于 BFS 按层扩展，因此先遍历到的点，一定是最短路径。

1. 初始化

• 创建 distance 矩阵：所有 0 设为 0，所有 1 设为 Infinity。
• 将所有 0 的坐标入队，作为 BFS 起点。

2. BFS 计算最短距离

• 依次从队列中取出 (i, j) 坐标：
  • 尝试向 四个方向 传播（上、下、左、右）。
  • 若 distance[nx][ny] > distance[i][j] + 1，说明发现更短路径，则：
    • 更新 distance[nx][ny]
    • 把 (nx, ny) 加入队列，后续继续扩展。

3. 返回 distance 矩阵

• 经过 BFS 遍历后，distance 矩阵即为 最短路径结果。

复杂度分析

• 时间复杂度：O(m * n)，BFS 每次遍历四个方向，每个点最多被访问一次（入队）。
• 空间复杂度：O(m * n)，需要 distance 矩阵存储答案，同时 queue 最坏情况可能存 m * n 个元素。

代码

/**
 * @param {number[][]} mat
 * @return {number[][]}
 */
var updateMatrix = function (mat) {
	const m = mat.length;
	const n = mat[0].length;
	let distance = Array.from({ length: m }, () => Array(n).fill(Infinity));

	const dirc = [
		[1, 0],
		[-1, 0],
		[0, 1],
		[0, -1]
	];
	let queue = [];

	// 预处理：找到所有 0，作为 BFS 起点
	for (let i = 0; i < m; i++) {
		for (let j = 0; j < n; j++) {
			if (mat[i][j] === 0) {
				distance[i][j] = 0;
				queue.push([i, j]);
			}
		}
	}

	while (queue.length) {
		const [i, j] = queue.shift();
		for (let [dx, dy] of dirc) {
			const nx = i + dx;
			const ny = j + dy;
			if (
				nx >= 0 &&
				nx < m &&
				ny >= 0 &&
				ny < n &&
				distance[nx][ny] > distance[i][j] + 1
			) {
				distance[nx][ny] = distance[i][j] + 1;
				// 只有更新的点才入队，进行下一层遍历，避免重复计算
				queue.push([nx, ny]);
			}
		}
	}

	return distance;
};

相关题目

题号	标题	题解	标签	难度	力扣
1730	获取食物的最短路径 🔒		广度优先搜索 数组 矩阵	🟠	🀄️ 🔗
2123	使矩阵中的 1 互不相邻的最小操作数 🔒		图 数组 矩阵	🔴	🀄️ 🔗
2482	行和列中一和零的差值		数组 矩阵 模拟	🟠	🀄️ 🔗