563. 二叉树的坡度

🟢 🔖 树 深度优先搜索 二叉树 🔗 力扣open in new window LeetCodeopen in new window

题目

Given the root of a binary tree, return the sum of every tree node 's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Example 1:

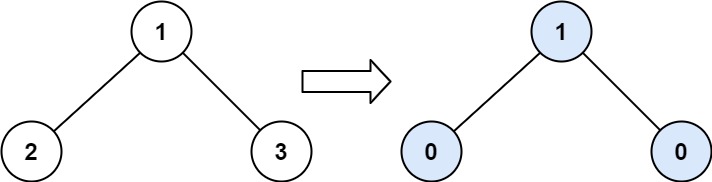
Input: root = [1,2,3]
Output: 1
Explanation:
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2:

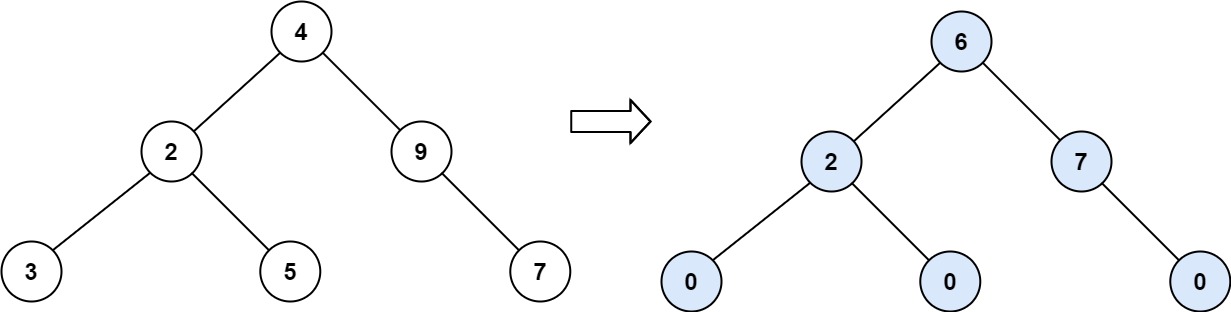
Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation:
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3:

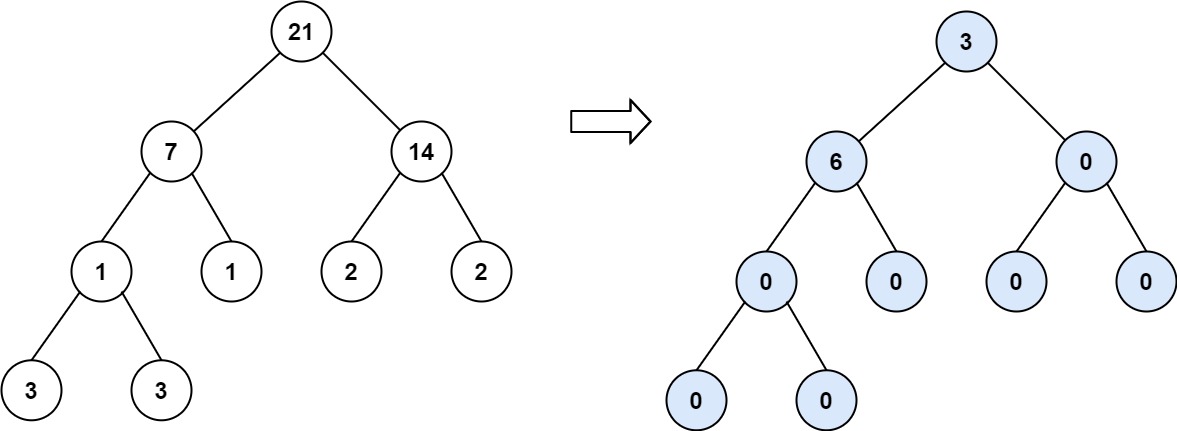
Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

The number of nodes in the tree is in the range [0, 104].
-1000 <= Node.val <= 1000

题目大意

给你一个二叉树的根节点 root ，计算并返回 整个树 的坡度。

一个树的节点的坡度 定义即为，该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话，左子树的节点之和为 0 ；没有右子树的话也是一样。空结点的坡度是 0 。

整个树 的坡度就是其所有节点的坡度之和。

示例 1：

输入： root = [1,2,3]
输出： 1
解释：
节点 2 的坡度：|0-0| = 0（没有子节点）
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 1 的坡度：|2-3| = 1（左子树就是左子节点，所以和是 2 ；右子树就是右子节点，所以和是 3 ）
坡度总和：0 + 0 + 1 = 1

示例 2：

输入： root = [4,2,9,3,5,null,7]
输出： 15
解释：
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 5 的坡度：|0-0| = 0（没有子节点）
节点 7 的坡度：|0-0| = 0（没有子节点）
节点 2 的坡度：|3-5| = 2（左子树就是左子节点，所以和是 3 ；右子树就是右子节点，所以和是 5 ）
节点 9 的坡度：|0-7| = 7（没有左子树，所以和是 0 ；右子树正好是右子节点，所以和是 7 ）
节点 4 的坡度：|(3+5+2)-(9+7)| = |10-16| = 6（左子树值为 3、5 和 2 ，和是 10 ；右子树值为 9 和 7 ，和是 16 ）
坡度总和：0 + 0 + 0 + 2 + 7 + 6 = 15

示例 3：

输入： root = [21,7,14,1,1,2,2,3,3]
输出： 9

提示：

树中节点数目的范围在 [0, 104] 内
-1000 <= Node.val <= 1000

解题思路

使用后序遍历（先计算子树，再处理当前节点）的方法：

初始化变量 totalTilt = 0，用于存储整个树的坡度之和
定义一个辅助函数 dfs(node)：
- 如果当前节点为 null，直接返回 0，因为空节点的坡度和节点值的和都为 0。
- 递归地计算左子树的节点值之和 leftSum。
- 递归地计算右子树的节点值之和 rightSum。
- 利用左子树和右子树的节点值之和计算当前节点的坡度，累加到全局变量 totalTilt 中。
- 返回以当前节点为根的子树节点值的和。
调用辅助函数 dfs(root)，从根节点开始递归，返回整个树的坡度之和

复杂度分析

时间复杂度：O(n)，其中 n 是树中节点的数量，每个节点只会被遍历一次。
空间复杂度：O(n)，空间复杂度由递归深度决定，最坏情况下（链式树）为 O(n)，平均情况下（平衡树）为 O(log n)。

代码

/**
 * @param {TreeNode} root
 * @return {number}
 */
var findTilt = function (root) {
	let totalTilt = 0; // 用于存储整个树的坡度之和

	// 辅助函数：返回以当前节点为根的子树节点值的和
	const dfs = (node) => {
		if (!node) return 0; // 空节点返回 0

		// 递归计算左子树和右子树的节点值之和
		const leftSum = dfs(node.left);
		const rightSum = dfs(node.right);

		// 累加当前节点的坡度
		totalTilt += Math.abs(leftSum - rightSum);

		// 返回当前子树的节点值之和
		return leftSum + rightSum + node.val;
	};

	dfs(root); // 从根节点开始递归
	return totalTilt; // 返回整个树的坡度之和
};

563. 二叉树的坡度

# 563. 二叉树的坡度

# 题目

# 题目大意

# 解题思路

# 复杂度分析

# 代码

# 相关题目

563. 二叉树的坡度

题目

题目大意

解题思路

复杂度分析

代码

相关题目