1466. 重新规划路线

🟠   🔖  深度优先搜索 广度优先搜索 图  🔗 力扣 LeetCode

题目

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Example 1:

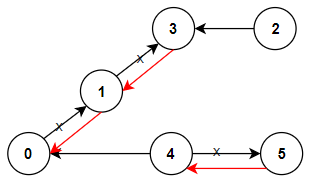
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]

Output: 3

Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]

Output: 2

Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3:

Input: n = 3, connections = [[1,0],[2,0]]

Output: 0

Constraints:

• 2 <= n <= 5 * 10^4
• connections.length == n - 1
• connections[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi

题目大意

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：


输入： n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]

输出： 3

解释： 更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2：


输入： n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]

输出： 2

解释： 更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3：

输入： n = 3, connections = [[1,0],[2,0]]

输出： 0

提示：

• 2 <= n <= 5 * 10^4
• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

解题思路

可以将问题转化为一个 无向图的遍历问题：

• 题目给出一个包含 n 个城市和 n-1 条道路的 有向图，这些道路可能不是都指向城市 0。
• 目标是调整最少的道路方向，使所有路径都能从任意城市到达城市 0，使城市 0 成为唯一的根节点。

1. 新建一个 无向图，将每条有向边 [city1, city2] 转化为无向边，并用正负 1 记录边的方向：
   • 如果边的方向是 从 city1 指向 city2，标记为正向边 (+1)。
   • 如果边的方向是 从 city2 指向 city1，标记为反向边 (-1)。
2. 使用 深度优先搜索 (DFS) 或 广度优先搜索 (BFS) 遍历图：
   • 从城市 0 出发，沿着所有邻居递归遍历。
   • 如果遇到正向边，则需要反转边，计数加 1。
   • 如果是反向边，则无需反转。
3. 遍历完成后，统计需要反转的边的数量。

复杂度分析

• 时间复杂度： O(n)，构建邻接表需要 O(n)，DFS 或 BFS 遍历需要 O(n)。
• 空间复杂度： O(n)，邻接表、访问数组和递归栈/队列的大小都是 O(n)。

代码

深度优先搜索 (DFS) 解法

/**
 * @param {number} n
 * @param {number[][]} connections
 * @return {number}
 */
var minReorder = function (n, connections) {
	// 构建邻接表，记录边的方向
	let graph = new Array(n).fill().map(() => new Array());
	for (let [city1, city2] of connections) {
		graph[city1].push([city2, 1]); // 正向边
		graph[city2].push([city1, -1]); // 反向边
	}

	let count = 0;
	const visited = new Array(n).fill(false);

	const dfs = (node) => {
		visited[node] = true;
		for (let [neighbor, direction] of graph[node]) {
			if (!visited[neighbor]) {
				if (direction === 1) count++; // 正向边需要反转
				dfs(neighbor);
			}
		}
	};

	dfs(0); // 从节点 0 开始 DFS 遍历
	return count;
};

广度优先搜索 (BFS) 解法

/**
 * @param {number} n
 * @param {number[][]} connections
 * @return {number}
 */
var minReorder = function (n, connections) {
	// 构建邻接表，记录边的方向
	let graph = new Array(n).fill().map(() => new Array());
	for (let [city1, city2] of connections) {
		graph[city1].push([city2, 1]); // 正向边
		graph[city2].push([city1, -1]); // 反向边
	}

	let count = 0;
	const visited = new Array(n).fill(false);
	const queue = [0];
	visited[0] = true;

	while (queue.length) {
		const node = queue.shift();
		for (let [neighbor, direction] of graph[node]) {
			if (!visited[neighbor]) {
				if (direction === 1) count++; // 正向边需要反转
				visited[neighbor] = true;
				queue.push(neighbor);
			}
		}
	}

	return count;
};

相关题目

题号	标题	题解	标签	难度	力扣
2858	可以到达每一个节点的最少边反转次数		深度优先搜索 广度优先搜索 图 1+	🔴	🀄️ 🔗