1462. 课程表 IV
1462. 课程表 IV
🟠 🔖 深度优先搜索 广度优先搜索 图 拓扑排序 🔗 力扣 LeetCode
题目
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.
- For example, the pair
[0, 1]indicates that you have to take course0before you can take course1.
Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.
Return a boolean arrayanswer , whereanswer[j]is the answer to thejth query.
Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0.
Course 0 is not a prerequisite of course 1, but the opposite is true.
Example 2:
Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites, and each course is independent.
Example 3:
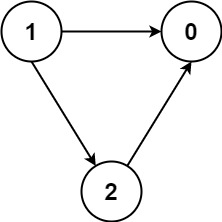
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]
Constraints:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= numCourses - 1ai != bi- All the pairs
[ai, bi]are unique. - The prerequisites graph has no cycles.
1 <= queries.length <= 10^40 <= ui, vi <= numCourses - 1ui != vi
题目大意
你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程,你必须 先选 ai 课程。
- 有的课会有直接的先修课程,比如如果想上课程
1,你必须先上课程0,那么会以[0,1]数对的形式给出先修课程数对。
先决条件也可以是 间接 的。如果课程 a 是课程 b 的先决条件,课程 b 是课程 c 的先决条件,那么课程 a 就是课程 c 的先决条件。
你也得到一个数组 queries ,其中 queries[j] = [uj, vj]。对于第 j 个查询,您应该回答课程 uj 是否是课程 vj 的先决条件。
返回一个布尔数组 answer ,其中 answer[j] 是第 j 个查询的答案。
示例 1:

输入: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出:[false,true]
解释:[1, 0] 数对表示在你上课程 0 之前必须先上课程 1。
课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例 2:
输入: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出:[false,false]
解释: 没有先修课程对,所以每门课程之间是独立的。
示例 3:

输入: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出:[true,true]
提示:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= numCourses - 1ai != bi- 每一对
[ai, bi]都 不同 - 先修课程图中没有环。
1 <= queries.length <= 10^40 <= ui, vi <= numCourses - 1ui != vi
解题思路
本问题可以抽象为判断有向图中某节点是否能到达另一个节点。典型的解决方案包括:
- 深度优先搜索 (DFS) 或广度优先搜索 (BFS): 每次查询时从源节点出发进行搜索。
- 预处理所有可达性 (Floyd-Warshall 或动态规划): 通过预处理将所有节点间的可达性存储,降低查询时间复杂度。
由于查询次数可能较多,预处理方法通常更高效。
思路一:Floyd-Warshall 算法
- 用一个二维布尔数组
reachable,其中reachable[i][j]表示节点i是否能到达节点j。 - 根据
prerequisites初始化reachable数组。 - 使用 Floyd-Warshall 算法进行三层循环,检查通过中间节点是否可以连通,更新可达性。
- 对每个查询直接查表即可。
复杂度分析
- 时间复杂度:
O(n^3),其中n是课程数量。 - 空间复杂度:
O(n^2)。
思路二:深度优先搜索 (DFS) + 缓存
算法步骤:
- 将
prerequisites转换为邻接表。 - 使用 DFS 判断节点
u是否能到达节点v。 - 使用缓存 (memoization) 优化多次查询的重复计算。
复杂度分析
- 时间复杂度:
O(V + E + Q * V),其中V是课程数量,E是先修关系数量,Q是查询数量。 - 空间复杂度:
O(V + E)。
思路三:拓扑排序 + 动态规划
- 使用拓扑排序计算课程的拓扑序列。
- 通过动态规划计算每门课程的所有先修课程集合。
- 直接查询先修集合即可。
复杂度分析
- 时间复杂度:
O(V + E + Q * V)。 - 空间复杂度:
O(V^2)。
代码
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function (numCourses, prerequisites, queries) {
const reachable = Array.from({ length: numCourses }, () =>
Array(numCourses).fill(false)
);
// Initialize direct prerequisites
for (const [u, v] of prerequisites) {
reachable[u][v] = true;
}
// Floyd-Warshall to find all reachable pairs
for (let k = 0; k < numCourses; k++) {
for (let i = 0; i < numCourses; i++) {
for (let j = 0; j < numCourses; j++) {
if (reachable[i][k] && reachable[k][j]) {
reachable[i][j] = true;
}
}
}
}
// Answer queries
return queries.map(([u, v]) => reachable[u][v]);
};
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function (numCourses, prerequisites, queries) {
const graph = Array.from({ length: numCourses }, () => []);
const memo = Array.from({ length: numCourses }, () => new Map());
// Build the graph
for (const [u, v] of prerequisites) {
graph[u].push(v);
}
// DFS function to check if u can reach v
const dfs = (u, v) => {
if (u === v) return true;
if (memo[u].has(v)) return memo[u].get(v);
for (const neighbor of graph[u]) {
if (dfs(neighbor, v)) {
memo[u].set(v, true);
return true;
}
}
memo[u].set(v, false);
return false;
};
// Answer each query
return queries.map(([u, v]) => dfs(u, v));
};
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function (numCourses, prerequisites, queries) {
const graph = Array.from({ length: numCourses }, () => []);
const indegree = Array(numCourses).fill(0);
const prereq = Array.from({ length: numCourses }, () => new Set());
// Build the graph and calculate indegrees
for (const [u, v] of prerequisites) {
graph[u].push(v);
indegree[v]++;
}
// Perform topological sort
const queue = [];
for (let i = 0; i < numCourses; i++) {
if (indegree[i] === 0) {
queue.push(i);
}
}
while (queue.length > 0) {
const course = queue.shift();
for (const next of graph[course]) {
prereq[next] = new Set([...prereq[next], ...prereq[course], course]);
indegree[next]--;
if (indegree[next] === 0) {
queue.push(next);
}
}
}
// Answer queries
return queries.map(([u, v]) => prereq[v].has(u));
};
