1448. 统计二叉树中好节点的数目

🟠   🔖  树 深度优先搜索 广度优先搜索 二叉树  🔗 力扣 LeetCode

题目

Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example 1:

Input: root = [3,1,4,3,null,1,5]

Output: 4

Explanation: Nodes in blue are good.

Root Node (3) is always a good node.

Node 4 -> (3,4) is the maximum value in the path starting from the root.

Node 5 -> (3,4,5) is the maximum value in the path

Node 3 -> (3,1,3) is the maximum value in the path.

Example 2:

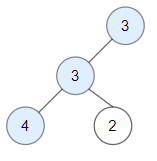
Input: root = [3,3,null,4,2]

Output: 3

Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Example 3:

Input: root = [1]

Output: 1

Explanation: Root is considered as good.

Constraints:

• The number of nodes in the binary tree is in the range [1, 10^5].
• Each node's value is between [-10^4, 10^4].

题目大意

给你一棵根为 root 的二叉树，请你返回二叉树中好节点的数目。

「好节点」X 定义为：从根到该节点 X 所经过的节点中，没有任何节点的值大于 X 的值。

示例 1：


输入： root = [3,1,4,3,null,1,5]

输出： 4

解释： 图中蓝色节点为好节点。

根节点 (3) 永远是个好节点。

节点 4 -> (3,4) 是路径中的最大值。

节点 5 -> (3,4,5) 是路径中的最大值。

节点 3 -> (3,1,3) 是路径中的最大值。

示例 2：


输入： root = [3,3,null,4,2]

输出： 3

解释： 节点 2 -> (3, 3, 2) 不是好节点，因为 "3" 比它大。

示例 3：

输入： root = [1]

输出： 1

解释： 根节点是好节点。

提示：

• 二叉树中节点数目范围是 [1, 10^5] 。
• 每个节点权值的范围是 [-10^4, 10^4] 。

解题思路

1. 树的深度优先搜索 (DFS)：

   • 使用 DFS 遍历二叉树。
   • 每次进入一个节点时，记录从根节点到当前节点路径上的最大值 max。
   • 如果当前节点值大于等于 max，则计数加 1，并更新路径上的最大值为当前节点值。

2. 递归处理每个子树：

   • 遍历当前节点的左子树和右子树，递归传递更新后的最大值 max。

3. 初始值选择：

   • 从根节点开始递归，初始路径最大值 max 设置为 -Infinity，因为根节点是好节点。

复杂度分析

• 时间复杂度：O(n)，其中 n 是节点总数，每个节点被访问一次。
• 空间复杂度：O()，递归栈的最大深度为树的高度 h，因此空间复杂度为 O(h)。
  • 在最坏情况下（链式结构），空间复杂度为 O(n)；
  • 在最佳情况下（完全平衡二叉树），空间复杂度为 O(log n)。

代码

/**
 * @param {TreeNode} root
 * @return {number}
 */
var goodNodes = function (root) {
	let count = 0; // 用于记录好节点数量

	// 定义递归函数
	const dfs = (node, max) => {
		if (!node) return; // 如果当前节点为空，直接返回

		// 判断当前节点是否是好节点
		if (node.val >= max) {
			count++; // 是好节点，计数加 1
			max = node.val; // 更新路径上的最大值
		}

		// 递归遍历左子树和右子树
		if (root.left) dfs(root.left, max);
		if (root.right) dfs(root.right, max);
	};

	dfs(root, -Infinity); // 从根节点开始，初始最大值为负无穷
	return count; // 返回好节点数量
};