1379. 找出克隆二叉树中的相同节点

🟢   🔖  树 深度优先搜索 广度优先搜索 二叉树  🔗 力扣 LeetCode

题目

Given two binary trees original and cloned and given a reference to a node target in the original tree.

The cloned tree is a copy of the original tree.

Return a reference to the same node in the cloned tree.

Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.

Example 1:

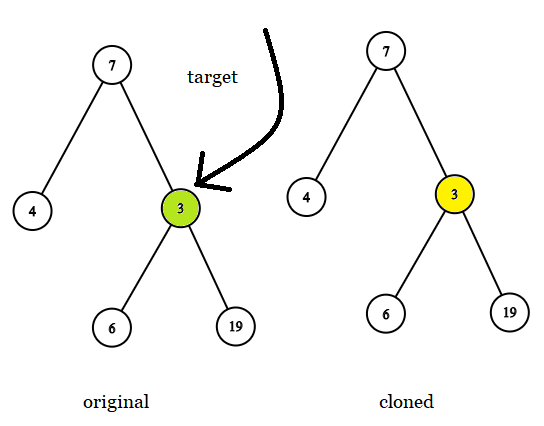
Input: tree = [7,4,3,null,null,6,19], target = 3

Output: 3

Explanation: In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.

Example 2:

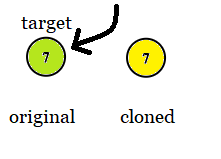
Input: tree = [7], target = 7

Output: 7

Example 3:

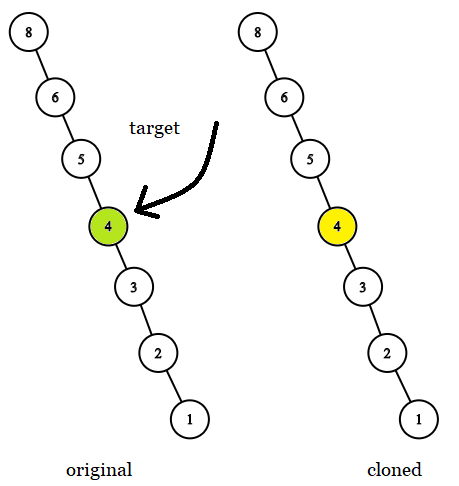
Input: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4

Output: 4

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• The values of the nodes of the tree are unique.
• target node is a node from the original tree and is not null.

Follow up: Could you solve the problem if repeated values on the tree are allowed?

题目大意

给你两棵二叉树，原始树 original 和克隆树 cloned，以及一个位于原始树 original 中的目标节点 target。

其中，克隆树 cloned 是原始树 original 的一个副本 。

请找出在树 cloned 中，与 target 相同的节点，并返回对该节点的引用（在 C/C++ 等有指针的语言中返回 节点指针，其他语言返回节点本身）。

注意： 你 不能 对两棵二叉树，以及 target 节点进行更改。只能 返回对克隆树 cloned 中已有的节点的引用。

示例 1:

输入: tree = [7,4,3,null,null,6,19], target = 3

输出: 3

解释: 上图画出了树 original 和 cloned。target 节点在树 original 中，用绿色标记。答案是树 cloned 中的黄颜色的节点（其他示例类似）。

示例 2:

输入: tree = [7], target = 7

输出: 7

示例 3:

输入: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4

输出: 4

提示：

• 树中节点的数量范围为 [1, 10^4] 。
• 同一棵树中，没有值相同的节点。
• target 节点是树 original 中的一个节点，并且不会是 null 。

进阶： 如果树中允许出现值相同的节点，将如何解答？

解题思路

1. 递归遍历二叉树：

   • 从根节点开始遍历 original 和 cloned 二叉树，同时保持相同的结构。
   • 当遍历到 original 的某个节点与 target 相同时，返回该节点在克隆树 cloned 中对应的节点。

2. 递归的基本条件：

   • 如果 original 为 null，说明已经到达树的末端，返回 null。
   • 如果当前 original 节点与 target 节点相同，则返回当前克隆树节点 cloned。
   • 如果 original 节点不等于 target，继续递归查找其左右子树。

3. 递归过程：

   • 从根节点开始，再检查左子树，若左子树没有找到目标，则再检查右子树。

复杂度分析

• 时间复杂度：O(n)，其中 n 是树的节点数，在最坏的情况下，需要遍历整个二叉树。
• 空间复杂度：O(h)，其中 h 是树的高度，由于递归使用栈，最深的递归深度为树的高度。

代码

/**
 * @param {TreeNode} original
 * @param {TreeNode} cloned
 * @param {TreeNode} target
 * @return {TreeNode}
 */
var getTargetCopy = function (original, cloned, target) {
	if (!original) return null; // 如果原树为空，返回null
	if (original == target) {
		return cloned; // 如果找到了目标节点，返回克隆树中的对应节点
	}
	// 递归查找左子树和右子树
	return (
		getTargetCopy(original.left, cloned.left, target) ||
		getTargetCopy(original.right, cloned.right, target)
	);
};