1312. 让字符串成为回文串的最少插入次数

🔴   🔖  字符串 动态规划  🔗 力扣 LeetCode

题目

Given a string s. In one step you can insert any character at any index of the string.

Return the minimum number of steps to make s palindrome.

A Palindrome String is one that reads the same backward as well as forward.

Example 1:

Input: s = "zzazz"

Output: 0

Explanation: The string "zzazz" is already palindrome we do not need any insertions.

Example 2:

Input: s = "mbadm"

Output: 2

Explanation: String can be "mbdadbm" or "mdbabdm".

Example 3:

Input: s = "leetcode"

Output: 5

Explanation: Inserting 5 characters the string becomes "leetcodocteel".

Constraints:

• 1 <= s.length <= 500
• s consists of lowercase English letters.

题目大意

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

「回文串」是正读和反读都相同的字符串。

s 中所有字符都是小写字母。

解题思路

这个问题可以使用动态规划来解决。可以定义一个二维数组 dp，其中 dp[i][j] 表示将字符串的子串 s[i...j] 变成回文串所需的最少插入次数。

1. 状态转移方程：

• 当字符 s[i] 等于 s[j] 时，表示 s[i...j] 已经是回文串，不需要插入，因此 dp[i][j] = dp[i+1][j-1]。
• 当字符 s[i] 不等于 s[j] 时，我们需要在 s[i...j] 的两端插入字符，使得插入后的子串 s[i...j] 是回文串，因此 dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1。
  • 为什么不是 dp[i][j] = dp[i+1][j-1] + 2 ？
  • 因为 s[i...j-1] 或 s[i+1...j] 有可能是回文串，不需要插入，如：s[i...j] = "xaaaaa" 时，s[i+1...j] = "aaaaa" 本身就是回文串；
  • 所以无脑插入两次肯定是可以让 s[i..j] 变成回文串，但是不一定是插入次数最少的；
  • 正确的做法是，先将 s[i..j-1] 或者 s[i+1..j] 变成回文串，然后取二者中插入次数少的情况，再加一；

if (s[i] === s[j]) {
	dp[i][j] = dp[i + 1][j - 1];
} else {
	dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
}

2. 初始化： 对角线上的元素 dp[i][i] 均为 0，因为单个字符已经是回文串。

3. 动态规划遍历： 在计算 dp[i][j] 时，需要先确保 dp[i+1][j-1] 已经计算过，因此需要按照区间长度从小到大的顺序遍历。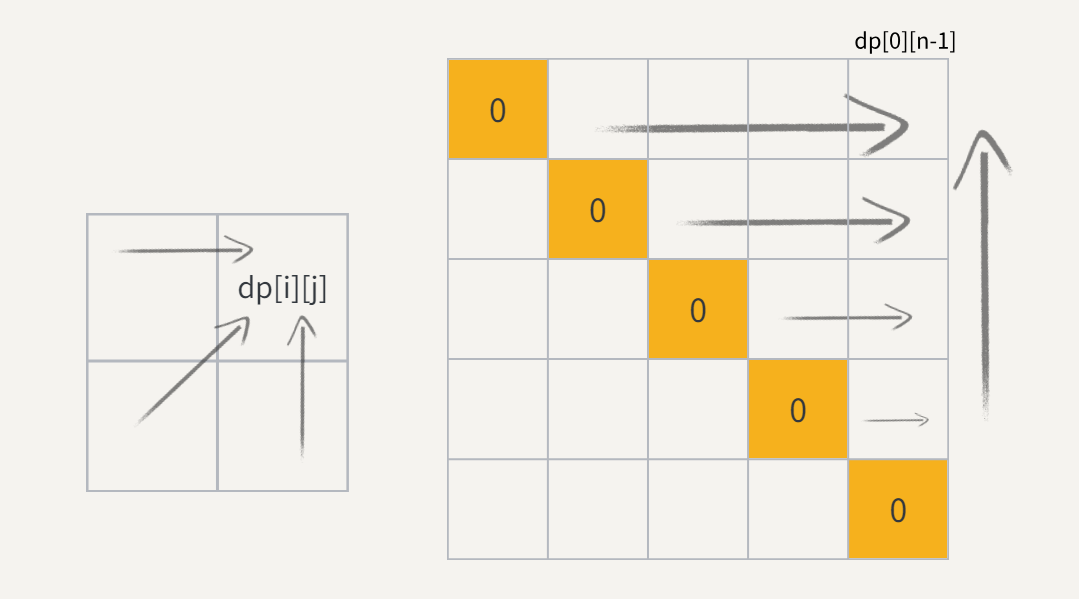

   

4. 返回结果： 最终结果存储在 dp[0][n-1] 中，其中 n 是字符串的长度。

复杂度分析

• 时间复杂度：O(n^2)，其中 n 是字符串的长度，动态规划数组的大小为 n^2。

• 空间复杂度：O(n^2)，使用了一个二维动态规划数组。

代码

/**
 * @param {string} s
 * @return {number}
 */
var minInsertions = function (s) {
	const n = s.length;
	let dp = new Array(n).fill(0).map((i) => new Array(n).fill(0));
	for (let i = n - 2; i >= 0; i--) {
		for (let j = i + 1; j < n; j++) {
			if (s[i] == s[j]) {
				dp[i][j] = dp[i + 1][j - 1];
			} else {
				dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
			}
		}
	}
	return dp[0][n - 1];
};

相关题目

题号	标题	题解	标签	难度	力扣
2193	得到回文串的最少操作次数		贪心 树状数组 双指针 1+	🔴	🀄️ 🔗