1266. 访问所有点的最小时间

🟢   🔖  几何 数组 数学  🔗 力扣 LeetCode

题目

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return _theminimum time in seconds to visit all the points in the order given by _points.

You can move according to these rules:

• In 1 second, you can either:
  • move vertically by one unit,
  • move horizontally by one unit, or
  • move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
• You have to visit the points in the same order as they appear in the array.
• You are allowed to pass through points that appear later in the order, but these do not count as visits.

Example 1:

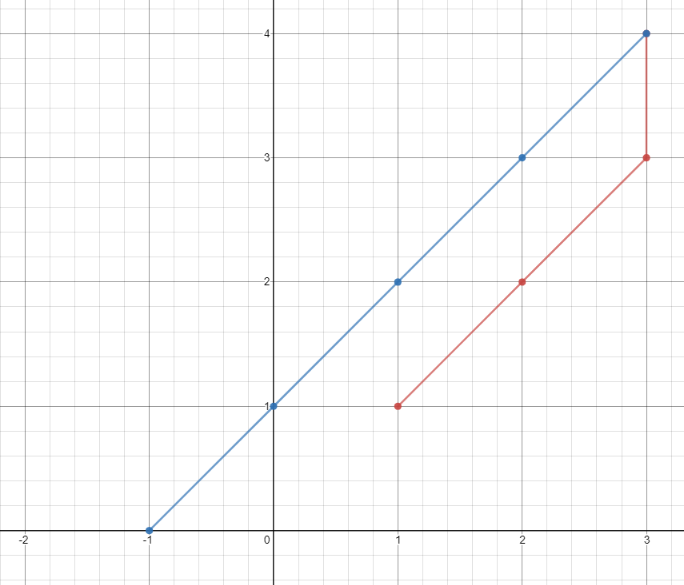
Input: points = [[1,1],[3,4],[-1,0]]

Output: 7

Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]

Time from [1,1] to [3,4] = 3 seconds

Time from [3,4] to [-1,0] = 4 seconds

Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]

Output: 5

Constraints:

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

题目大意

平面上有 n 个点，点的位置用整数坐标表示 points[i] = [xi, yi] 。请你计算访问所有这些点需要的 最小时间 （以秒为单位）。

你需要按照下面的规则在平面上移动：

• 每一秒内，你可以：

  • 沿水平方向移动一个单位长度，或者
  • 沿竖直方向移动一个单位长度，或者
  • 跨过对角线移动 sqrt(2) 个单位长度（可以看作在一秒内向水平和竖直方向各移动一个单位长度）。

• 必须按照数组中出现的顺序来访问这些点。

• 在访问某个点时，可以经过该点后面出现的点，但经过的那些点不算作有效访问。

示例 1：


输入： points = [[1,1],[3,4],[-1,0]]

输出： 7

解释： 一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]

从 [1,1] 到 [3,4] 需要 3 秒

从 [3,4] 到 [-1,0] 需要 4 秒

一共需要 7 秒

示例 2：

输入： points = [[3,2],[-2,2]]

输出： 5

提示：

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

解题思路

在二维平面上，从一个点到另一个点的最短时间是两个坐标差值的 最大值。

如果水平差值 dx 和竖直差值 dy 的较大值是 max(dx, dy)，则对角线可以覆盖较小的差值，剩下的差值需要水平或竖直方向补足。

1. 遍历点的列表，从第一个点开始访问。
2. 对于每对相邻点：
   • 计算水平距离 dx 和竖直距离 dy；
   • 增加 max(dx, dy) 到结果中。
3. 返回最终结果。

复杂度分析

• 时间复杂度：O(n)，其中 n 是点的数量，遍历 points 列表计算相邻点之间的距离。
• 空间复杂度：O(1)，仅使用常数额外空间存储变量。

代码

/**
 * @param {number[][]} points
 * @return {number}
 */
var minTimeToVisitAllPoints = function (points) {
	let res = 0;
	for (let i = 1; i < points.length; i++) {
		let dx = Math.abs(points[i - 1][0] - points[i][0]);
		let dy = Math.abs(points[i - 1][1] - points[i][1]);
		res += Math.max(dx, dy);
	}
	return res;
};