1261. 在受污染的二叉树中查找元素
1261. 在受污染的二叉树中查找元素
🟠 Medium 🔖 树 深度优先搜索 广度优先搜索 设计 哈希表 二叉树 🔗 力扣 LeetCode
题目
Given a binary tree with the following rules:
root.val == 0- If
treeNode.val == xandtreeNode.left != null, thentreeNode.left.val == 2 * x + 1 - If
treeNode.val == xandtreeNode.right != null, thentreeNode.right.val == 2 * x + 2
Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.
Implement the FindElements class:
FindElements(TreeNode* root)Initializes the object with a contaminated binary tree and recovers it.bool find(int target)Returnstrueif thetargetvalue exists in the recovered binary tree.
Example 1:
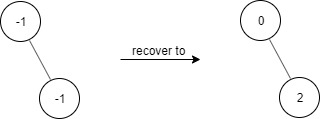
Input
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
Output
[null,false,true]
Explanation
FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True
Example 2:
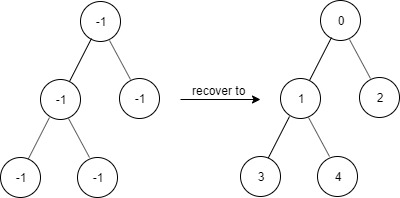
Input
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
Output
[null,true,true,false]
Explanation
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False
Example 3:
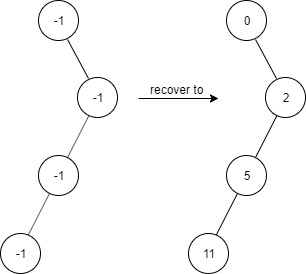
Input
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
Output
[null,true,false,false,true]
Explanation
FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True
Constraints:
TreeNode.val == -1- The height of the binary tree is less than or equal to
20 - The total number of nodes is between
[1, 104] - Total calls of
find()is between[1, 104] 0 <= target <= 10^6
题目大意
给出一个满足下述规则的二叉树:
root.val == 0- 如果
treeNode.val == x且treeNode.left != null,那么treeNode.left.val == 2 * x + 1 - 如果
treeNode.val == x且treeNode.right != null,那么treeNode.right.val == 2 * x + 2
现在这个二叉树受到「污染」,所有的 treeNode.val 都变成了 -1。
请你先还原二叉树,然后实现 FindElements 类:
FindElements(TreeNode* root)用受污染的二叉树初始化对象,你需要先把它还原。bool find(int target)判断目标值target是否存在于还原后的二叉树中并返回结果。
示例 1:

输入:
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
输出:
[null,false,true]
解释:
FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True
示例 2:

输入:
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
输出:
[null,true,true,false]
解释:
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False
示例 3:

输入:
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
输出:
[null,true,false,false,true]
解释:
FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True
提示:
TreeNode.val == -1- 二叉树的高度不超过
20 - 节点的总数在
[1, 10^4]之间 - 调用
find()的总次数在[1, 10^4]之间 0 <= target <= 10^6
解题思路
- 恢复树的值
- 使用 深度优先搜索(DFS) 遍历树:
- 从
root开始,将其val设为0。 - 递归更新
left和right子节点的值:left.val = 2 * parent.val + 1right.val = 2 * parent.val + 2
- 同时将计算出的值存入
Set以便快速查询。
- 从
- 实现
find(target)
- 由于使用
Set存储所有有效值,因此find(target)只需执行set.has(target)查找即可。
复杂度分析
时间复杂度:
- 构造
FindElements类:需要遍历整棵树,并使用 DFS 递归遍历每个节点一次,因此时间复杂度为O(n),其中n为二叉树节点数。 find(target)查询:直接在Set里查找target,哈希表查找的时间复杂度为O(1)。
- 构造
空间复杂度:
O(n),额外存储Set需要O(n)的空间。
代码
/**
* @param {TreeNode} root
*/
var FindElements = function (root) {
this.set = new Set(); // 存储所有恢复后的值
this.dfs(root, 0);
};
/**
* @param {number} target
* @return {boolean}
*/
FindElements.prototype.find = function (target) {
return this.set.has(target);
};
/**
* @param {TreeNode} root
* @param {number} num
*/
FindElements.prototype.dfs = function (root, num) {
if (!root) return;
root.val = num; // 恢复当前节点的值
this.set.add(num); // 记录该值到 Set 里
this.dfs(root.left, num * 2 + 1);
this.dfs(root.right, num * 2 + 2);
};
