1260. 二维网格迁移

🟢   🔖  数组 矩阵 模拟  🔗 力扣 LeetCode

题目

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

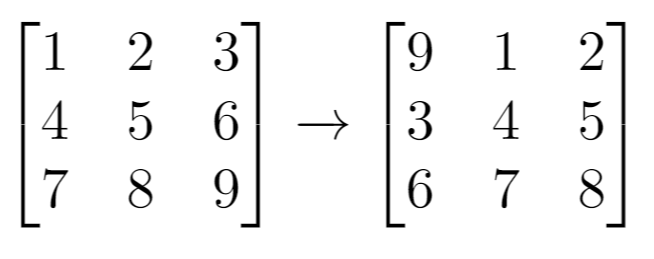
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1

Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

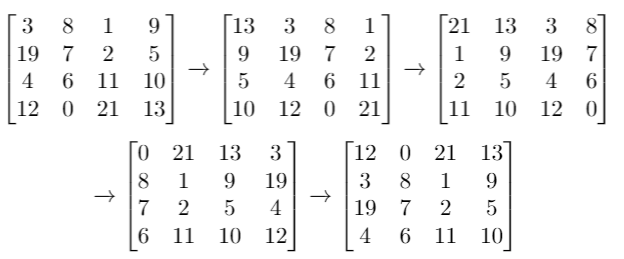
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4

Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9

Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

题目大意

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

• 位于 grid[i][j]（j < n - 1）的元素将会移动到 grid[i][j + 1]。
• 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
• 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格 。

示例 1：


输入： grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1

输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：


输入： grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4

输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

示例 3：

输入： grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9

输出：[[1,2,3],[4,5,6],[7,8,9]]

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

解题思路

思路一：直接映射

思路：
通过直接计算目标矩阵中每个元素在源矩阵中的位置来完成操作：

1. 计算矩阵的大小 m * n；
2. 遍历矩阵中的每个元素，利用公式计算其在目标位置的行列索引：
   • 新的行索引：(i + floor((j + k) / n)) % m；
   • 新的列索引：(j + k) % n；
3. 创建一个新的矩阵 res 来保存结果。

复杂度分析

• 时间复杂度： O(m * n)
• 空间复杂度： O(m * n)

---

思路二：矩阵一维化 + 翻转法

将矩阵看作一个一维数组，对其整体进行「环形右移」：

1. 将矩阵的二维坐标索引转化为一维索引；
2. 借助翻转数组的技巧，分三步完成右移：
   • 翻转整个数组；
   • 翻转前 k 个元素；
   • 翻转后 x - k 个元素；
3. 最后将数组恢复为矩阵。

复杂度分析

• 时间复杂度： O(m * n)
• 空间复杂度： O(1)，原地操作，无额外空间开销。

代码

直接映射

/**
 * @param {number[]} heights
 * @param {number[][]} queries
 * @return {number[]}
 */
var shiftGrid = function (grid, k) {
	const m = grid.length;
	const n = grid[0].length;
	let res = new Array(m).fill().map(() => new Array(n));
	for (let i = 0; i < m; i++) {
		for (let j = 0; j < n; j++) {
			res[(i + Math.floor((j + k) / n)) % m][(j + k) % n] = grid[i][j];
		}
	}
	return res;
};

矩阵一维化 + 翻转法

/**
 * @param {number[]} heights
 * @param {number[][]} queries
 * @return {number[]}
 */
var shiftGrid = function (grid, k) {
	const m = grid.length;
	const n = grid[0].length;
	const x = m * n;
	k %= x;

	const reverse = (a, b) => {
		while (a < b) {
			[grid[Math.floor(a / n)][a % n], grid[Math.floor(b / n)][b % n]] = [
				grid[Math.floor(b / n)][b % n],
				grid[Math.floor(a / n)][a % n]
			];
			a++;
			b--;
		}
	};

	reverse(0, x - 1); // 翻转整个数组
	reverse(0, k - 1); // 翻转前 k 个元素
	reverse(k, x - 1); // 翻转后 x-k 个元素

	return grid;
};