跳至主要內容

1252. 奇数值单元格的数目

1252. 奇数值单元格的数目

🟢   🔖  数组 数学 模拟  🔗 力扣open in new window LeetCodeopen in new window

题目

There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], do both of the following:

  1. Increment all the cells on row ri.
  2. Increment all the cells on column ci.

Given m, n, and indices, return _the number of odd-valued cells in the matrix after applying the increment to all locations in _indices.

Example 1:

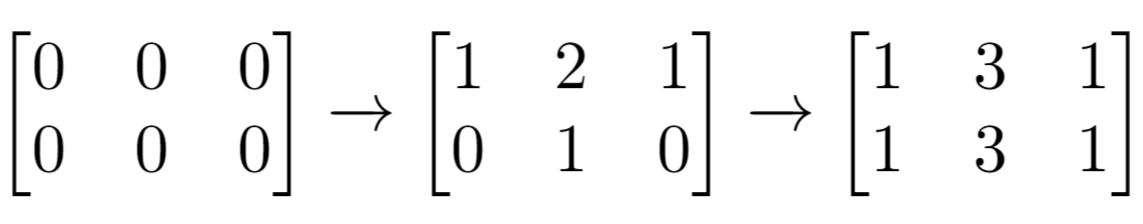
Input: m = 2, n = 3, indices = [[0,1],[1,1]]

Output: 6

Explanation: Initial matrix = [[0,0,0],[0,0,0]].

After applying first increment it becomes [[1,2,1],[0,1,0]].

The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.

Example 2:

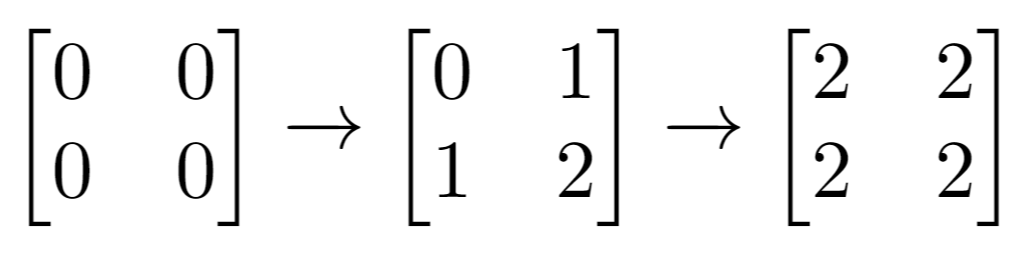
Input: m = 2, n = 2, indices = [[1,1],[0,0]]

Output: 0

Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.

Constraints:

  • 1 <= m, n <= 50
  • 1 <= indices.length <= 100
  • 0 <= ri < m
  • 0 <= ci < n

Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?

题目大意

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

  1. ri 行上的所有单元格，加 1 。
  2. ci 列上的所有单元格，加 1 。

给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例 1：

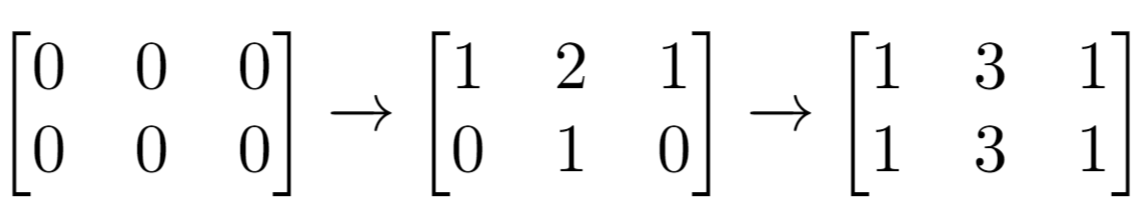
输入： m = 2, n = 3, indices = [[0,1],[1,1]]

输出： 6

解释： 最开始的矩阵是 [[0,0,0],[0,0,0]]。

第一次增量操作后得到 [[1,2,1],[0,1,0]]。

最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2：

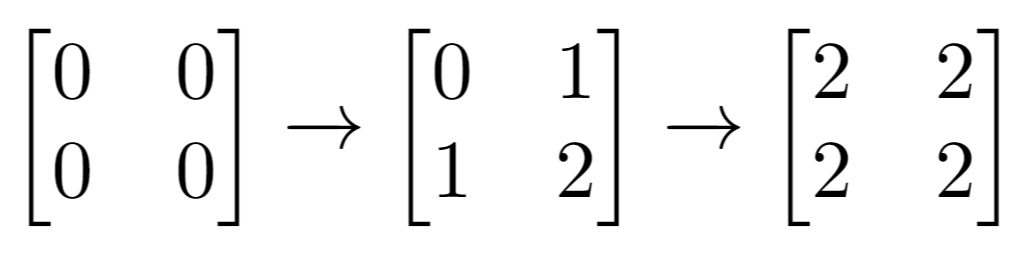
输入： m = 2, n = 2, indices = [[1,1],[0,0]]

输出： 0

解释： 最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示：

  • 1 <= m, n <= 50
  • 1 <= indices.length <= 100
  • 0 <= ri < m
  • 0 <= ci < n

进阶： 你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗？

解题思路

  1. 行和列的影响分离：

    • 每次对 r 行加 1 的操作，只会增加该行对应元素的值；
    • 每次对 c 列加 1 的操作，只会增加该列对应元素的值。
    • 所以，可以分别统计行和列的增量，并通过求和来确定最终值是否为奇数。

  2. 奇偶性判断：

    • 一个矩阵元素是否为奇数，仅取决于其所在行和列的增量奇偶性。
    • 如果某个元素所在行的增量 row[i] 和列的增量 col[j] 之和是奇数，则该元素是奇数。
    • 行奇数与列偶数交叉的元素为奇数。
    • 行偶数与列奇数交叉的元素为奇数。

  3. 公式化结果：

    • 设 oddRow 和 evenRow 分别为奇数行和偶数行的数量；
    • 设 oddCol 和 evenCol 分别为奇数列和偶数列的数量；
    • 矩阵中奇数值元素的数量为：oddRow * evenCol + evenRow * oddCol

  4. 实现步骤：

    • 初始化两个数组 row 和 col，分别记录每行和每列的增量；
    • 遍历 indices，更新 row 和 col 的计数；
    • 遍历 row 和 col，统计奇偶行和列的数量；
    • 根据公式计算奇数值元素的总数。

复杂度分析

  • 时间复杂度：O(k + m + n)，
    • 遍历 indices 更新 row 和 col，时间复杂度为 O(k)，其中 k 是 indices 的长度。
    • 分别遍历 row 和 col 统计奇偶行和列，时间复杂度为 O(m + n)。
  • 空间复杂度：O(m + n)，row 和 col 的大小分别为 O(m) 和 O(n)。

代码

/**
 * @param {number} m
 * @param {number} n
 * @param {number[][]} indices
 * @return {number}
 */
var oddCells = function (m, n, indices) {
	let row = new Array(m).fill(0);
	let col = new Array(n).fill(0);

	// 更新行和列的增量
	for (let [r, c] of indices) {
		row[r]++;
		col[c]++;
	}

	// 统计奇偶行和列的数量
	let oddRow = 0,
		evenRow = 0;
	for (let num of row) {
		if (num % 2 === 0) {
			evenRow++;
		} else {
			oddRow++;
		}
	}

	let oddCol = 0,
		evenCol = 0;
	for (let num of col) {
		if (num % 2 === 0) {
			evenCol++;
		} else {
			oddCol++;
		}
	}

	// 根据公式计算奇数值元素总数
	return oddRow * evenCol + evenRow * oddCol;
};
Copyright © 2025 2xiao