897. 递增顺序搜索树

🟢   🔖  栈 树 深度优先搜索 二叉搜索树 二叉树  🔗 力扣 LeetCode

题目

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

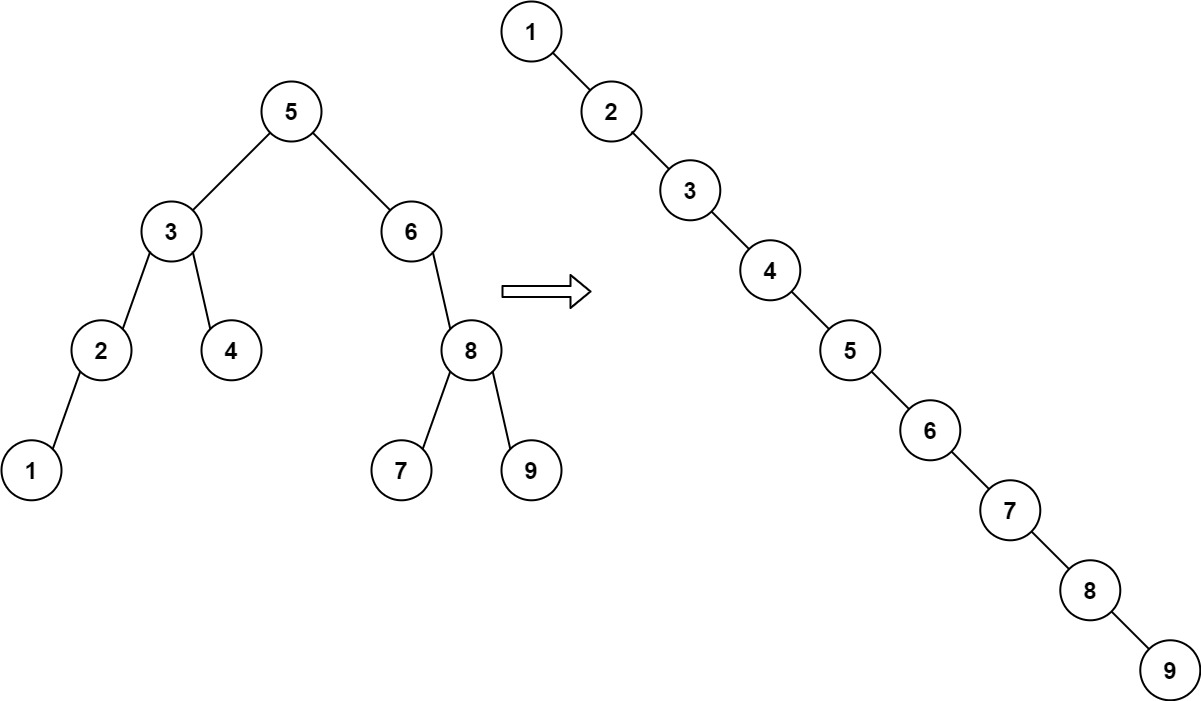
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]

Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

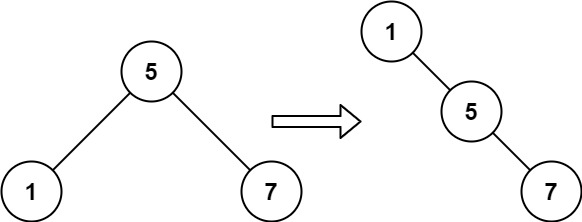
Input: root = [5,1,7]

Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

题目大意

给你一棵二叉搜索树的 root ，请你 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例 1：

输入： root = [5,3,6,2,4,null,8,1,null,null,null,7,9]

输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

示例 2：

输入： root = [5,1,7]

输出：[1,null,5,null,7]

提示：

• 树中节点数的取值范围是 [1, 100]
• 0 <= Node.val <= 1000

解题思路

二叉搜索树的中序遍历得到的结果是一个递增序列。

1. 使用一个 哑节点（dummy node）作为新树的起点。

2. 用一个指针 curr 记录当前新树的构造位置。

3. 中序遍历的每一步：

   • 将当前节点的左子节点清空（因为新树没有左子节点）。
   • 将当前节点连接到新树的右子节点。
   • 更新 curr 为当前节点。

4. 返回结果：哑节点的右子节点即为新树的根节点。

复杂度分析

• 时间复杂度：O(n)，其中 n 是树中节点的数量，中序遍历访问每个节点一次。
• 空间复杂度：O(h)，其中 h 是树的高度，递归栈的深度取决于树的高度，最坏情况下为 O(h)。

代码

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var increasingBST = function (root) {
	let dummy = new TreeNode(-1); // 创建一个哑节点作为新树的起点
	let curr = dummy;

	const inorder = (node) => {
		if (!node) return;
		inorder(node.left); // 递归左子树
		node.left = null; // 清理左子节点
		curr.right = node; // 将当前节点接到新树的右子树
		curr = node; // 更新当前指针
		inorder(node.right); // 递归右子树
	};

	inorder(root);

	return dummy.right; // 返回哑节点的右子节点，即新树的根
};