867. 转置矩阵

🟢   🔖  数组 矩阵 模拟  🔗 力扣 LeetCode

题目

Given a 2D integer array matrix, return thetranspose of matrix.

The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.

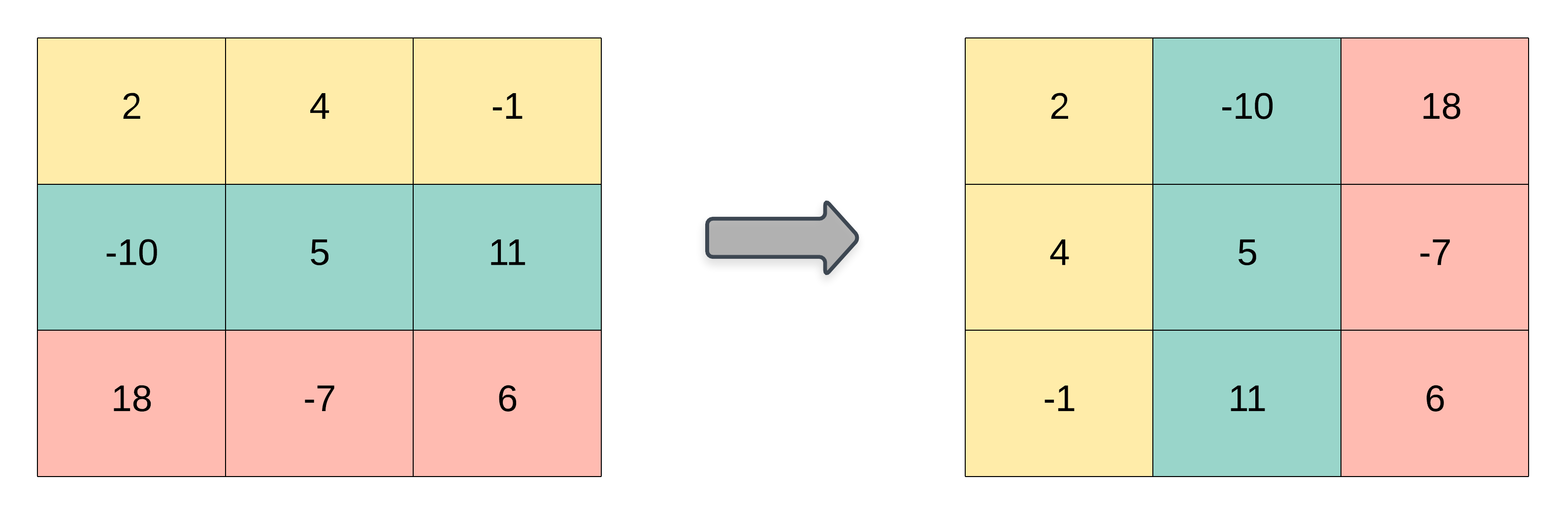
Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]

Output: [[1,4,7],[2,5,8],[3,6,9]]

Example 2:

Input: matrix = [[1,2,3],[4,5,6]]

Output: [[1,4],[2,5],[3,6]]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 10^5
• -10^9 <= matrix[i][j] <= 10^9

题目大意

给你一个二维整数数组 matrix， 返回 matrix 的 转置矩阵 。

矩阵的 转置 是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。

示例 1：

输入： matrix = [[1,2,3],[4,5,6],[7,8,9]]

输出：[[1,4,7],[2,5,8],[3,6,9]]

示例 2：

输入： matrix = [[1,2,3],[4,5,6]]

输出：[[1,4],[2,5],[3,6]]

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 10^5
• -10^9 <= matrix[i][j] <= 10^9

解题思路

• 获取原矩阵的行数 m 和列数 n。
• 初始化一个空矩阵 res，其尺寸为 n x m，用来存储转置后的结果。
• 遍历原矩阵的每个元素 matrix[i][j]，将其放到转置矩阵的相应位置 res[j][i]。
• 返回 res。

复杂度分析

• 时间复杂度：O(m * n)，其中 m 是原矩阵的行数，n 是原矩阵的列数。遍历矩阵中的每个元素一次。
• 空间复杂度：O(m * n)，创建了一个新的矩阵 res，其大小是 n x m。

代码

/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
var transpose = function (matrix) {
	// 获取原矩阵的行数 m 和列数 n
	const m = matrix.length;
	const n = matrix[0].length;

	// 创建转置矩阵，大小为 n x m
	let res = new Array(n).fill().map(() => new Array(m));

	// 遍历原矩阵，将元素放到转置矩阵对应的位置
	for (let i = 0; i < m; i++) {
		for (let j = 0; j < n; j++) {
			res[j][i] = matrix[i][j]; // 交换行列
		}
	}

	return res; // 返回转置后的矩阵
};