892. 三维形体的表面积

🟢   🔖  几何 数组 数学 矩阵  🔗 力扣 LeetCode

题目

You are given an n x n grid where you have placed some 1 x 1 x 1 cubes. Each value v = grid[i][j] represents a tower of v cubes placed on top of cell (i, j).

After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.

Return the total surface area of the resulting shapes.

Note: The bottom face of each shape counts toward its surface area.

Example 1:

Input: grid = [[1,2],[3,4]]

Output: 34

Example 2:

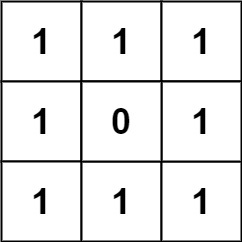
Input: grid = [[1,1,1],[1,0,1],[1,1,1]]

Output: 32

Example 3:

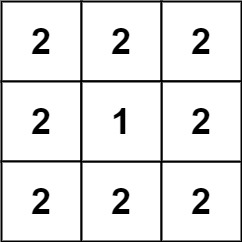
Input: grid = [[2,2,2],[2,1,2],[2,2,2]]

Output: 46

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

题目大意

给你一个 n * n 的网格 grid ，上面放置着一些 1 x 1 x 1 的正方体。每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。

放置好正方体后，任何直接相邻的正方体都会互相粘在一起，形成一些不规则的三维形体。

请你返回最终这些形体的总表面积。

注意： 每个形体的底面也需要计入表面积中。

示例 1：

输入： grid = [[1,2],[3,4]]

输出： 34

示例 2：

输入： grid = [[1,1,1],[1,0,1],[1,1,1]]

输出： 32

示例 3：

输入： grid = [[2,2,2],[2,1,2],[2,2,2]]

输出： 46

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

解题思路

1. 柱体的顶部和底部：

   • 如果柱体高度 grid[i][j] > 0，顶部和底部的表面积固定为 2。

2. 柱体的侧面：

   • 对于 (i, j) 位置的柱体，高度为 grid[i][j]，需要考虑与其相邻的四个方向（上、下、左、右）的柱体高度：
     • 若相邻位置的柱体高度比当前柱体低，只有超出的部分暴露，其大小为 grid[i][j] - grid[ni][nj]。
     • 如果相邻位置不存在柱体（越界情况），则该方向的侧面完全暴露，表面积为当前柱体的高度 grid[i][j]。

3. 遍历所有柱体：

   • 对于每个柱体 (i, j)，累加顶部、底部和四个方向的侧面暴露面积，最终得到总表面积。

复杂度分析

• 时间复杂度：O(n^2)，其中 n 是网格的边长，要遍历整个网格的每个位置。
• 空间复杂度：O(1)，只使用了常数额外空间。

代码

/**
 * @param {number[][]} grid
 * @return {number}
 */
var surfaceArea = function (grid) {
	const n = grid.length; // 网格大小
	const dirc = [
		[1, 0],
		[-1, 0],
		[0, 1],
		[0, -1]
	]; // 四个方向偏移量
	let res = 0;

	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			if (grid[i][j] > 0) {
				res += 2; // 顶部和底部面积

				// 遍历四个方向
				for (let [di, dj] of dirc) {
					const ni = i + di; // 相邻位置的行坐标
					const nj = j + dj; // 相邻位置的列坐标
					let nv = 0; // 相邻位置的柱体高度

					// 如果相邻位置在网格范围内，获取其高度
					if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
						nv = grid[ni][nj];
					}

					// 计算当前方向的暴露面积
					res += Math.max(grid[i][j] - nv, 0);
				}
			}
		}
	}

	return res; // 返回总表面积
};