812. 最大三角形面积

🟢   🔖  几何 数组 数学  🔗 力扣 LeetCode

题目

Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10^-5 of the actual answer will be accepted.

Example 1:

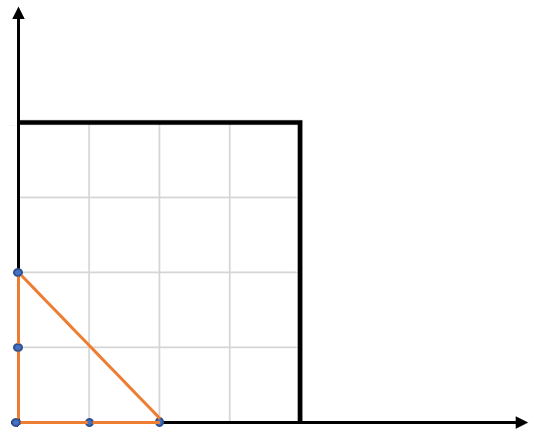
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]

Output: 2.00000

Explanation: The five points are shown in the above figure. The red triangle is the largest.

Example 2:

Input: points = [[1,0],[0,0],[0,1]]

Output: 0.50000

Constraints:

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• All the given points are unique.

题目大意

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10^-5 内的答案将会视为正确答案**。**

示例 1：

输入： points = [[0,0],[0,1],[1,0],[0,2],[2,0]]

输出： 2.00000

解释： 输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入： points = [[1,0],[0,0],[0,1]]

输出： 0.50000

提示：

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• 给出的所有点 互不相同

解题思路

这个问题要求我们计算给定一组点中，可以组成的最大三角形的面积。可以使用几何学中的 叉积公式 来计算三角形的面积。

1. 三角形面积的计算：

   对于三角形 ABC，其中三个点的坐标分别为 (Xa, Ya)、(Xb, Yb) 和 (Xc, Yc)，三角形的面积可以使用叉积公式计算：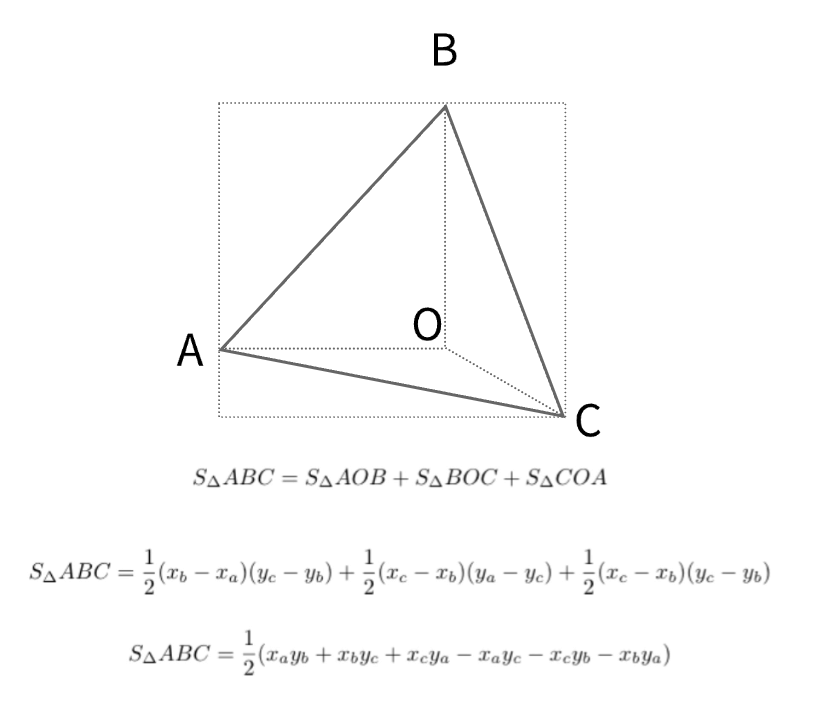

   

2. 遍历所有点组合：

   • 给定 points 数组，包含了若干二维坐标点。要找到最大的三角形面积，需要遍历所有可能的点三元组组合，并计算这些组合所形成的三角形面积。
   • 由于输入数组的长度较小（最大为 50），因此直接用三重循环遍历所有点组合是可行的。

3. 更新最大面积：

   • 每次计算一个三角形的面积后，更新当前的最大面积值。

复杂度分析

• 时间复杂度：O(n^3)，其中 n 是点的数量。有三重循环来遍历所有的点组合，由于题目中给定 n <= 50，这样复杂度是可以接受的。

• 空间复杂度：O(1)，只使用了常数空间来存储中间结果。

代码

/**
 * @param {number[][]} points
 * @return {number}
 */
var largestTriangleArea = function (points) {
	// 计算三角形面积的函数
	const getArea = (i, j, k) => {
		return (
			0.5 *
			Math.abs(
				i[0] * j[1] +
					j[0] * k[1] +
					k[0] * i[1] -
					j[0] * i[1] -
					k[0] * j[1] -
					i[0] * k[1]
			)
		);
	};

	const n = points.length;
	let res = 0; // 用来记录最大的三角形面积

	// 三重循环遍历所有点的三元组
	for (let i = 0; i < n; i++) {
		for (let j = i + 1; j < n; j++) {
			for (let k = j + 1; k < n; k++) {
				// 计算面积并更新最大面积
				res = Math.max(res, getArea(points[i], points[j], points[k]));
			}
		}
	}
	return res;
};

相关题目

题号	标题	题解	标签	难度	力扣
976	三角形的最大周长	[✓]	贪心 数组 数学 1+	🟢	🀄️ 🔗