883. 三维形体投影面积

🟢   🔖  几何 数组 数学 矩阵  🔗 力扣 LeetCode

题目

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).

We view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the "shadow" when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

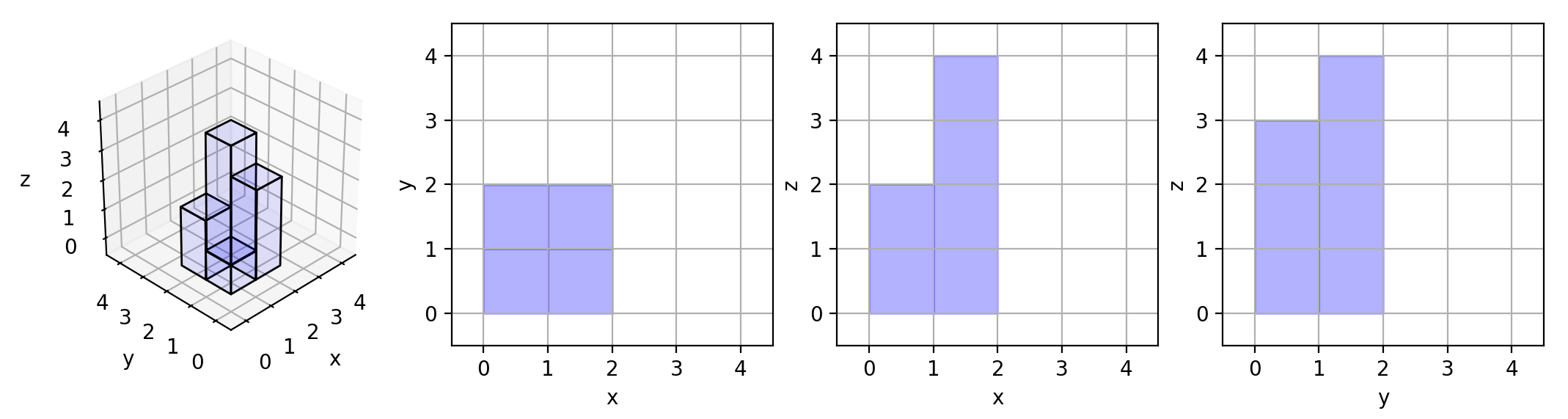
Input: grid = [[1,2],[3,4]]

Output: 17

Explanation: Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

Example 2:

Input: grid = [[2]]

Output: 5

Example 3:

Input: grid = [[1,0],[0,2]]

Output: 8

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

题目大意

在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的 投影 。

投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回 所有三个投影的总面积 。

示例 1：

输入：[[1,2],[3,4]]

输出： 17

解释： 这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 2:

输入： grid = [[2]]

输出： 5

示例 3：

输入：[[1,0],[0,2]]

输出： 8

提示：

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

解题思路

这个问题要求计算给定的 n x n 网格的三个投影面积，网格中的每个元素表示在该位置上的高度，投影面积是基于该网格的不同视角来计算的：

• 顶部投影面积：每个非零元素都会对面积做贡献，因此每个非零元素的投影在顶视图中占据一个单位的面积。
• 正面投影面积：每一行的最大值决定该行从正面看到的投影面积。例如，第 i 行的最大元素决定了该行的投影面积。
• 侧面投影面积：每一列的最大值决定该列从侧面看到的投影面积。例如，第 j 列的最大元素决定了该列的投影面积。

1. 遍历矩阵：由于矩阵的大小是 n x n，所以只需要遍历一次矩阵，在遍历行 grid[i][j] 时，可以通过 grid[j][i] 遍历列。
2. 顶部投影：对于每个位置 grid[i][j]，如果该值大于 0，投影面积加一。
3. 正面投影：对于每一行 i，找出该行的最大值 maxRow，将其添加到投影总面积中。
4. 侧面投影：对于每一列 j，找出该列的最大值 maxCol，将其添加到投影总面积中。
5. 返回结果：返回总的投影面积 total。

复杂度分析

• 时间复杂度：O(n^2)，其中 n 是网格的大小，需要遍历矩阵中的所有元素。
• 空间复杂度：O(1)，只用了常量空间来存储一些变量。

代码

/**
 * @param {number[][]} grid
 * @return {number}
 */
var projectionArea = function (grid) {
	const n = grid.length;
	let total = 0;

	// 遍历每一行，计算顶部投影、正面投影
	for (let i = 0; i < n; i++) {
		let maxRow = 0; // 当前行的最大值
		let maxCol = 0; // 当前列的最大值
		for (let j = 0; j < n; j++) {
			// 顶部投影：每个非零元素都会贡献一个面积
			if (grid[i][j] > 0) total++;

			// 正面投影：当前行的最大值
			maxRow = Math.max(maxRow, grid[i][j]);

			// 侧面投影：当前列的最大值
			maxCol = Math.max(maxCol, grid[j][i]);
		}
		// 将正面和侧面投影的最大值加入总面积
		total += maxRow + maxCol;
	}

	return total;
};