790. 多米诺和托米诺平铺

🟠   🔖  动态规划  🔗 力扣 LeetCode

题目

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

Input: n = 3

Output: 5

Explanation: The five different ways are show above.

Example 2:

Input: n = 1

Output: 1

Constraints:

• 1 <= n <= 1000

题目大意

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

输入: n = 3

输出: 5

解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1

输出: 1

提示：

• 1 <= n <= 1000

解题思路

这道题的核心在于如何利用动态规划来枚举所有可能的铺法。

如图所示：

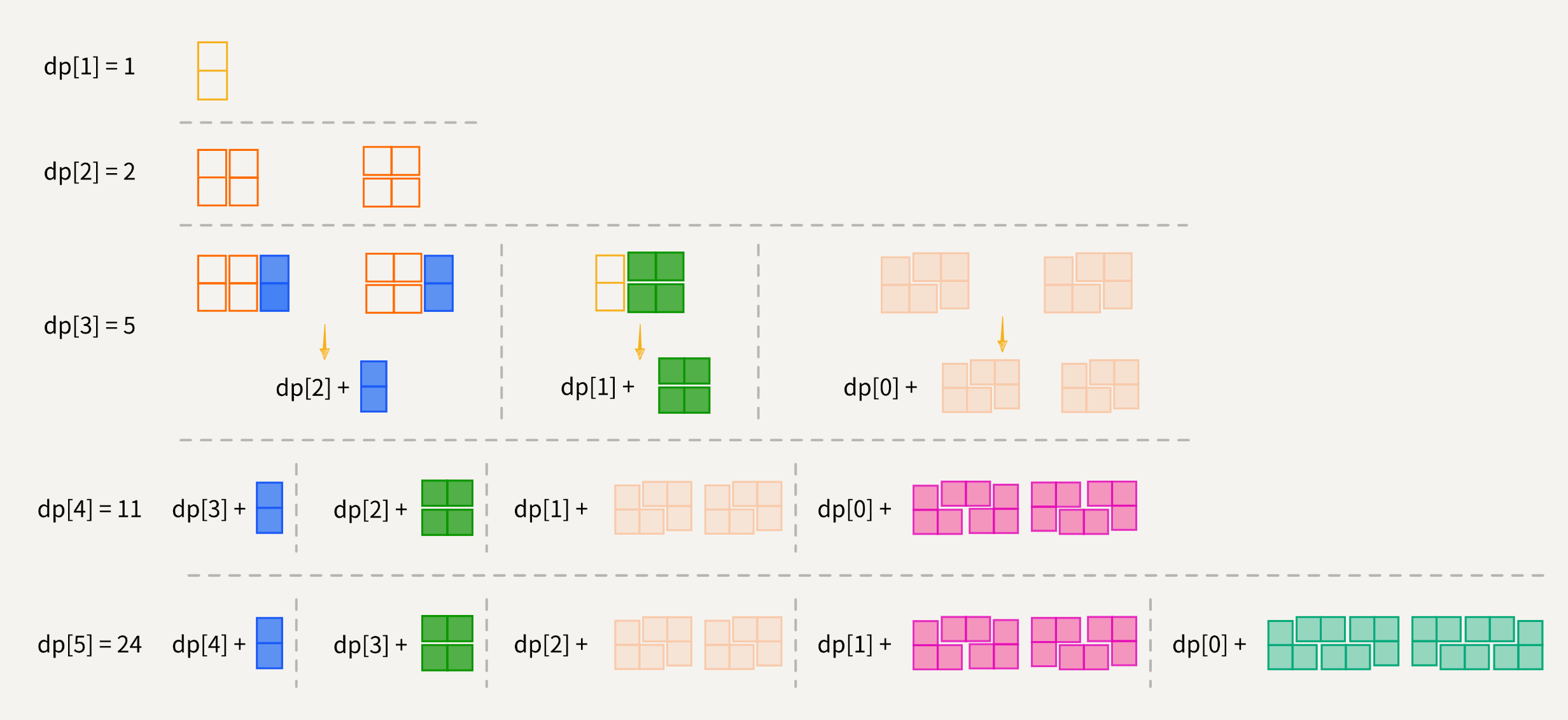
• dp[0] = 1：空棋盘有一种铺法。
• dp[1] = 1：一个 2 * 1 的棋盘只能用一个竖直的多米诺骨牌铺满。
• dp[2] = 2：两个竖直多米诺骨牌或两个水平多米诺骨牌。
• dp[3] = 5：
  • dp[3] = dp[2] + dp[1] + 2 * dp[0]
  • 在 dp[2] 后面加一个竖直的多米诺骨牌：2
  • 在 dp[1] 后面加两个水平的多米诺骨牌：1
  • 在 dp[0] 后面加两个 L 形托米诺骨牌：2
• dp[4] = 11：
  • dp[4] = dp[3] + dp[2] + 2 * dp[1] + 2 * dp[0]
  • 在 dp[3] 后面加一个竖直的多米诺骨牌：5
  • 在 dp[2] 后面加两个水平的多米诺骨牌：2
  • 在 dp[1] 后面加两个 L 形托米诺骨牌：2
  • 在 dp[0] 后面加一个水平的多米诺骨牌和两个 L 形托米诺骨牌：2
• dp[5] = 24：
  • dp[5] = dp[4] + dp[3] + 2 * dp[2] + 2 * dp[1] + 2 * dp[0]
  • 在 dp[4] 后面加一个竖直的多米诺骨牌：11
  • 在 dp[3] 后面加两个水平的多米诺骨牌：5
  • 在 dp[2] 后面加两个 L 形托米诺骨牌：4
  • 在 dp[1] 后面加一个水平的多米诺骨牌和两个 L 形托米诺骨牌：2
  • 在 dp[0] 后面加两个水平的多米诺骨牌和两个 L 形托米诺骨牌：2

由此可以得到递推关系：

dp[n] = dp[n-1] + dp[n-2] +  2 * (dp[n-3] + ... + d[0])
      = dp[n-1] + dp[n-2] + dp[n-3] + dp[n-3] + 2 * (dp[n-4] + ... + d[0])
      = dp[n-1] + dp[n-3] + (dp[n-2] + dp[n-3] + 2 * (dp[n-4] + ... + d[0]))
      = dp[n-1] + dp[n-3] + dp[n-1]
      = 2 * dp[n-1] + dp[n-3]

复杂度分析

• 时间复杂度：O(n)，动态规划需要遍历 n。

• 空间复杂度：

  • 常规 DP：需要存储 n + 1 个状态，空间复杂度为 O(n)。
  • 优化 DP：只需要三个变量，空间复杂度为 O(1)。

代码

动态规划

/**
 * @param {number} n
 * @return {number}
 */
var numTilings = function (n) {
	const MOD = 1e9 + 7;

	let dp = new Array(n + 1).fill(0);
	dp[0] = 1;
	dp[1] = 1;
	dp[2] = 2;

	for (let i = 3; i <= n; i++) {
		dp[i] = (2 * dp[i - 1] + dp[i - 3]) % MOD;
	}

	return dp[n];
};

动态规划（空间优化）

/**
 * @param {number} n
 * @return {number}
 */
var numTilings = function (n) {
	const MOD = 1e9 + 7;

	if (n === 0) return 1;
	if (n === 1) return 1;
	if (n === 2) return 2;

	let dp0 = 1,
		dp1 = 1,
		dp2 = 2;

	for (let i = 3; i <= n; i++) {
		let curr = (2 * dp2 + dp0) % MOD;
		dp0 = dp1;
		dp1 = dp2;
		dp2 = curr;
	}

	return dp2;
};