2481. 分割圆的最少切割次数

🟢   🔖  几何 数学  🔗 力扣 LeetCode

题目

A valid cut in a circle can be:

• A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or
• A cut that is represented by a straight line that touches one point on the edge of the circle and its center.

Some valid and invalid cuts are shown in the figures below.

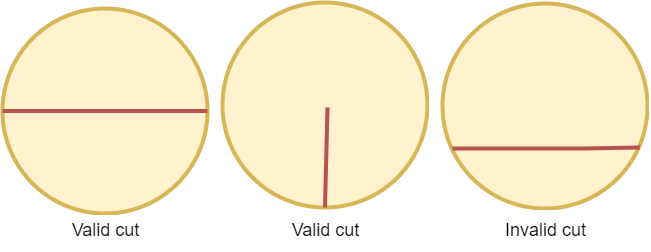
Given the integer n, return the minimum number of cuts needed to divide a circle into n equal slices.

Example 1:

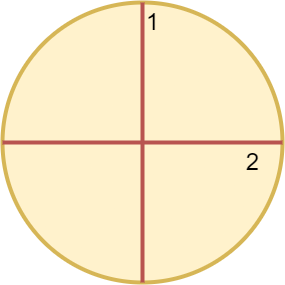
Input: n = 4

Output: 2

Explanation:

The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices.

Example 2:

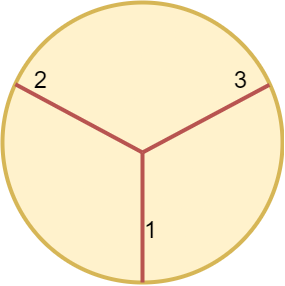
Input: n = 3

Output: 3

Explanation:

At least 3 cuts are needed to divide the circle into 3 equal slices.

It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape.

Also note that the first cut will not divide the circle into distinct parts.

Constraints:

• 1 <= n <= 100

题目大意

圆内一个 有效切割 ，符合以下二者之一：

• 该切割是两个端点在圆上的线段，且该线段经过圆心。
• 该切割是一端在圆心另一端在圆上的线段。

一些有效和无效的切割如下图所示。

给你一个整数 n ，请你返回将圆切割成相等的 n 等分的 最少 切割次数。

示例 1：

输入： n = 4

输出： 2

解释：

上图展示了切割圆 2 次，得到四等分。

示例 2：

输入： n = 3

输出： 3

解释：

最少需要切割 3 次，将圆切成三等分。

少于 3 次切割无法将圆切成大小相等面积相同的 3 等分。

同时可以观察到，第一次切割无法将圆切割开。

提示：

• 1 <= n <= 100

解题思路

题目要求计算 最少的切割次数，将一个 正 n 边形 切割成 n 个相等部分。我们可以发现：

• 当 n = 1 时，不需要切割，返回 0。
• 当 n 为偶数，我们可以用 n/2 条对角线切割成 n 份。
• 当 n 为奇数，我们至少需要 n 条线（每条切割一部分）。

复杂度分析

• 时间复杂度：O(1)，仅包含简单的条件判断和数学计算。
• 空间复杂度：O(1)，没有额外的数据结构。

代码

/**
 * @param {number} n
 * @return {number}
 */
var numberOfCuts = function (n) {
	if (n === 1) return 0;
	if (n % 2 == 0) return n / 2;
	return n;
};

相关题目

题号	标题	题解	标签	难度	力扣
2413	最小偶倍数		数学 数论	🟢	🀄️ 🔗
2579	统计染色格子数	[✓]	数学	🟠	🀄️ 🔗