2415. 反转二叉树的奇数层

🟠   🔖  树 深度优先搜索 广度优先搜索 二叉树  🔗 力扣 LeetCode

题目

Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.

• For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].

Return the root of the reversed tree.

A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.

The level of a node is the number of edges along the path between it and the root node.

Example 1:

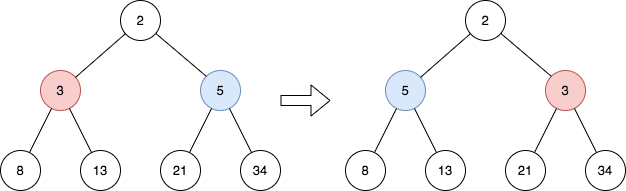
Input: root = [2,3,5,8,13,21,34]

Output: [2,5,3,8,13,21,34]

Explanation:

The tree has only one odd level.

The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.

Example 2:

Input: root = [7,13,11]

Output: [7,11,13]

Explanation:

The nodes at level 1 are 13, 11, which are reversed and become 11, 13.

Example 3:

Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]

Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]

Explanation:

The odd levels have non-zero values.

The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.

The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.

Constraints:

• The number of nodes in the tree is in the range [1, 214].
• 0 <= Node.val <= 10^5
• root is a perfect binary tree.

题目大意

给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

• 例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

示例 1：

输入： root = [2,3,5,8,13,21,34]

输出：[2,5,3,8,13,21,34]

解释：

这棵树只有一个奇数层。

在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

输入： root = [7,13,11]

输出：[7,11,13]

解释：

在第 1 层的节点分别是 13、11 ，反转后为 11、13 。

示例 3：

输入： root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]

输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]

解释： 奇数层由非零值组成。

在第 1 层的节点分别是 1、2 ，反转后为 2、1 。

在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

提示：

• 树中的节点数目在范围 [1, 214] 内
• 0 <= Node.val <= 10^5
• root 是一棵 完美 二叉树

解题思路

思路一：广度优先搜索（BFS）

1. 使用队列进行层序遍历。
2. 在遍历的过程中：
   • 如果是奇数层，反转交换当前层的节点值。
   • 将当前层节点的子节点插入队列。
   • 将当前层的节点出队。
3. 返回修改后的树。

复杂度分析

• 时间复杂度：O(n)
  • 每个节点访问一次，时间复杂度为 O(n)。
  • 反转每一奇数层的值，时间复杂度为 O(n)。
  • 总时间复杂度为 O(n)。
• 空间复杂度：O(n)，队列的最大长度为某一层的节点数，最坏情况下为 O(n)。

---

思路二：深度优先搜索（DFS）

1. 通过递归遍历树。
2. 当到达奇数层时，将左子树和右子树对应位置的值交换。
3. 对于偶数层，不进行任何操作。
4. 递归地同时遍历左子树和右子树。

复杂度分析

• 时间复杂度：O(n)，每个节点访问一次。
• 空间复杂度：O(log n)，递归栈的最大深度为树的高度，最坏情况下为O(log n)。

代码

广度优先搜索（BFS）

var reverseOddLevels = function (root) {
	if (!root) return root;

	let queue = [root]; // 初始化队列
	let level = 0; // 当前层数

	while (queue.length > 0) {
		const n = queue.length;

		// 遍历当前层
		for (let i = 0; i < n; i++) {
			// 如果当前是奇数层，交换两个节点的值
			if (level % 2 == 1 && i < n / 2) {
				let temp = queue[i].val;
				queue[i].val = queue[n - 1 - i].val;
				queue[n - 1 - i].val = temp;
			}

			// 下一层节点入队
			if (queue[i].left) queue.push(queue[i].left);
			if (queue[i].right) queue.push(queue[i].right);
		}
		queue = queue.slice(n);
		level++; // 进入下一层
	}

	return root;
};

深度优先搜索（DFS）

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var reverseOddLevels = function (root) {
	const dfs = (left, right, level) => {
		if (!left || !right) return;

		// 如果当前是奇数层，交换两个节点的值
		if (level % 2 == 0) {
			let temp = left.val;
			left.val = right.val;
			right.val = temp;
		}

		// 递归下一层
		dfs(left.left, right.right, level + 1);
		dfs(left.right, right.left, level + 1);
	};

	// 从第 1 层开始（根节点为第 0 层）
	dfs(root.left, root.right, 0);
	return root;
};

相关题目

题号	标题	题解	标签	难度	力扣
226	翻转二叉树	[✓]	树 深度优先搜索 广度优先搜索 1+	🟢	🀄️ 🔗