2471. 逐层排序二叉树所需的最少操作数目

🟠   🔖  树 广度优先搜索 二叉树  🔗 力扣 LeetCode

题目

You are given the root of a binary tree with unique values.

In one operation, you can choose any two nodes at the same level and swap their values.

Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.

The level of a node is the number of edges along the path between it and the root node .

Example 1:

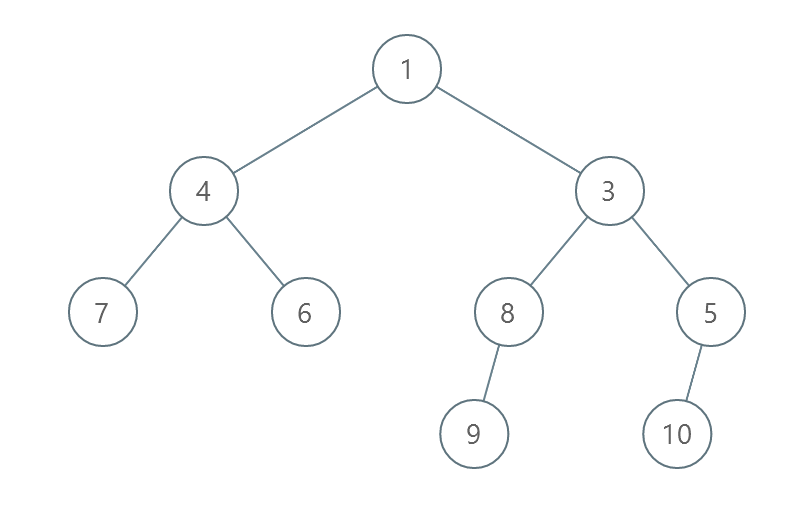
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]

Output: 3

Explanation:

• Swap 4 and 3. The 2nd level becomes [3,4].
• Swap 7 and 5. The 3rd level becomes [5,6,8,7].
• Swap 8 and 7. The 3rd level becomes [5,6,7,8].

We used 3 operations so return 3.

It can be proven that 3 is the minimum number of operations needed.

Example 2:

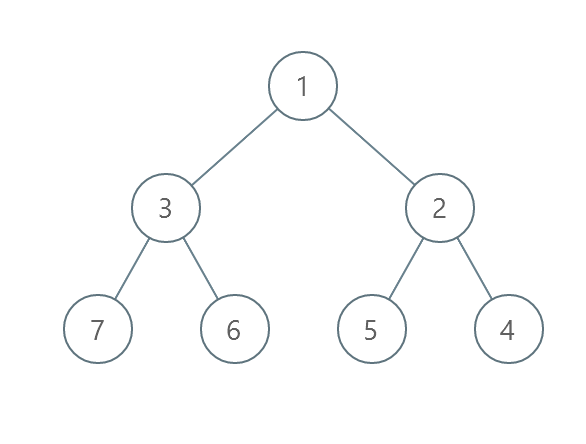
Input: root = [1,3,2,7,6,5,4]

Output: 3

Explanation:

• Swap 3 and 2. The 2nd level becomes [2,3].
• Swap 7 and 4. The 3rd level becomes [4,6,5,7].
• Swap 6 and 5. The 3rd level becomes [4,5,6,7].

We used 3 operations so return 3.

It can be proven that 3 is the minimum number of operations needed.

Example 3:

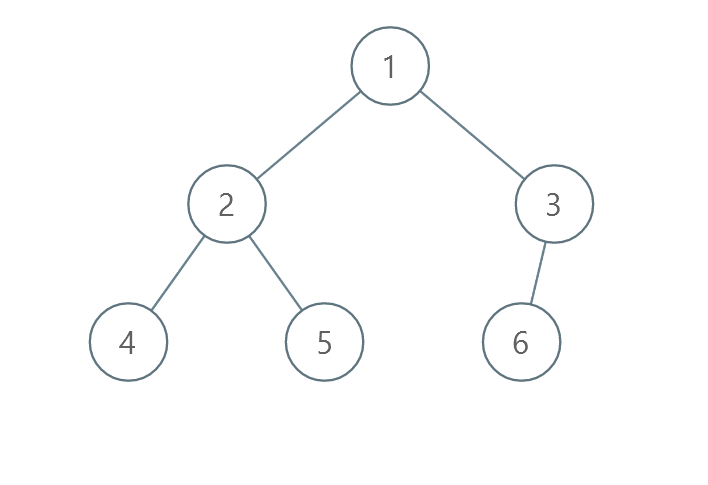
Input: root = [1,2,3,4,5,6]

Output: 0

Explanation: Each level is already sorted in increasing order so return 0.

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 10^5
• All the values of the tree are unique.

题目大意

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

输入： root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]

输出： 3

解释：

• 交换 4 和 3 。第 2 层变为 [3,4] 。
• 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
• 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。

共计用了 3 步操作，所以返回 3 。

可以证明 3 是需要的最少操作数目。

示例 2 ：

输入： root = [1,3,2,7,6,5,4]

输出： 3

解释： - 交换 3 和 2 。第 2 层变为 [2,3] 。

• 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
• 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。

共计用了 3 步操作，所以返回 3 。

可以证明 3 是需要的最少操作数目。

示例 3 ：

输入： root = [1,2,3,4,5,6]

输出： 0

解释： 每一层已经按递增顺序排序，所以返回 0 。

提示：

• 树中节点的数目在范围 [1, 105] 。
• 1 <= Node.val <= 10^5
• 树中的所有值 互不相同 。

解题思路

1. 使用层序遍历获取每一层节点的值

   • 二叉树可以按层访问，每一层的节点值组成一个数组。
   • 使用队列来实现层序遍历，按顺序遍历节点，将每一层的节点值存入数组中。

2. 计算数组排序所需的最少交换次数

   • 对于每一层的节点值数组，目标是将其排序为递增序列。
   • 我们需要一个辅助函数 getMinSwaps 来计算排序一个数组所需的最少交换次数。

3. getMinSwaps 计算最少交换次数

   1. 先将数组从小到大进行排序。
   2. 记录每个元素在目标数组（排序后的数组）中的位置。
   3. 遍历当前数组，如果当前元素不在其目标位置：
      • 找到当前元素的目标位置，与该位置的元素进行交换。
      • 更新当前数组，直到该元素在正确位置。
   4. 每次交换增加一次计数，最终返回总交换次数。

4. 遍历二叉树的每一层，将每一层排序所需的交换次数，累加到总次数中。

复杂度分析

• 时间复杂度：O(n log k)
  • 层序遍历，每个节点访问一次，时间复杂度为 O(n)，其中 n 是树的节点数量。
  • 排序与交换，每一层最多有 O(n) 个节点，计算交换次数的复杂度为 O(k log k)，其中 k 是当前层的节点数。
  • 所有层的总复杂度为 O(n log k)（k 是最大层的节点数）。
  • 总时间复杂度：O(n log k)。
• 空间复杂度：O(k)，其中 k 是每层的最大节点数。
  • 层序遍历需要一个队列，空间复杂度为 O(k)；
  • 排序需要额外的数组和哈希表，空间复杂度为 O(k)。

代码

/**
 * @param {TreeNode} root
 * @return {number}
 */
var minimumOperations = function (root) {
	// 初始化队列和总交换次数
	let queue = [root];
	let totalSwaps = 0;

	// 层序遍历
	while (queue.length) {
		const len = queue.length;
		let values = [];

		// 遍历当前层的节点
		for (let i = 0; i < len; i++) {
			const node = queue.shift();
			values.push(node.val);
			// 如果有左右子节点，加入队列
			if (node.left) queue.push(node.left);
			if (node.right) queue.push(node.right);
		}

		// 计算当前层的最少交换次数并累加
		totalSwaps += getMinSwaps(values);
	}

	return totalSwaps;
};

/**
 * 计算排序所需的最少交换次数
 * @param {number[]} arr
 * @return {number}
 */
var getMinSwaps = function (arr) {
	let target = [...arr].sort((a, b) => a - b); // 排序后的目标数组
	let pos = new Map(); // 记录目标位置
	for (let i = 0; i < target.length; i++) {
		pos.set(target[i], i);
	}

	let swaps = 0;
	for (let i = 0; i < target.length; i++) {
		// 如果当前元素不在正确位置
		while (arr[i] !== target[i]) {
			swaps++;
			const targetPos = pos.get(arr[i]); // 获取目标位置
			// 交换当前元素和目标位置的元素
			let temp = arr[i];
			arr[i] = arr[targetPos];
			arr[targetPos] = temp;
		}
	}

	return swaps;
};

相关题目

题号	标题	题解	标签	难度	力扣
102	二叉树的层序遍历	[✓]	树 广度优先搜索 二叉树	🟠	🀄️ 🔗
2360	图中的最长环		深度优先搜索 图 拓扑排序	🔴	🀄️ 🔗