跳至主要內容

2458. 移除子树后的二叉树高度

2458. 移除子树后的二叉树高度open in new window

🔴   🔖  树 深度优先搜索 广度优先搜索 数组 二叉树  🔗 力扣open in new window LeetCodeopen in new window

题目

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

  • Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an arrayanswer of sizem whereanswer[i]is the height of the tree after performing theith query.

Note :

  • The queries are independent, so the tree returns to its initial state after each query.
  • The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

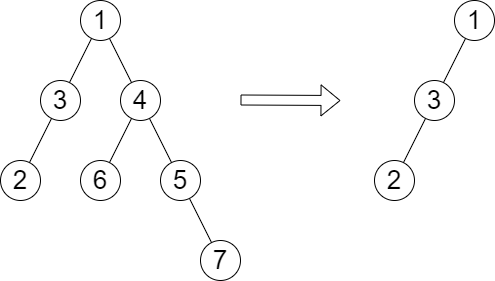
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]

Output: [2]

Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.

The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

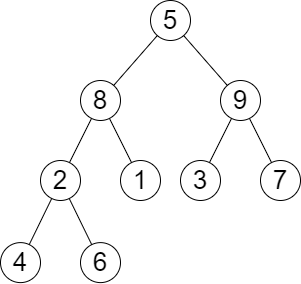
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]

Output: [3,2,3,2]

Explanation: We have the following queries:

  • Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
  • Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
  • Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
  • Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

  • The number of nodes in the tree is n.
  • 2 <= n <= 10^5
  • 1 <= Node.val <= n
  • All the values in the tree are unique.
  • m == queries.length
  • 1 <= m <= min(n, 104)
  • 1 <= queries[i] <= n
  • queries[i] != root.val

题目大意

给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个 独立 的查询，其中第 i 个查询你需要执行以下操作：

  • 从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。

返回一个长度为 m 的数组 **answer ** ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

  • 查询之间是独立的，所以在每个查询执行后，树会回到其 初始 状态。
  • 树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

输入： root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]

输出：[2]

解释： 上图展示了从树中移除以 4 为根节点的子树。

树的高度是 2（路径为 1 -> 3 -> 2）。

示例 2：

输入： root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]

输出：[3,2,3,2]

解释： 执行下述查询：

  • 移除以 3 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 4）。
  • 移除以 2 为根节点的子树。树的高度变为 2（路径为 5 -> 8 -> 1）。
  • 移除以 4 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 6）。
  • 移除以 8 为根节点的子树。树的高度变为 2（路径为 5 -> 9 -> 3）。

提示：

  • 树中节点的数目是 n
  • 2 <= n <= 10^5
  • 1 <= Node.val <= n
  • 树中的所有值 互不相同
  • m == queries.length
  • 1 <= m <= min(n, 10^4)
  • 1 <= queries[i] <= n
  • queries[i] != root.val

解题思路

树的高度是指从根节点到叶子节点的最长路径上的边数，使用深度优先搜索（DFS）来计算树的高度。

  1. 存储节点信息：

    • 使用一个哈希表（heightMap）来存储每个节点的高度和深度，键为节点的值，值为一个数组，包含节点的高度和深度 [height, depth]。

  2. 层级信息的存储：

    • 使用另一个哈希表（levelsMap）来存储每一层的最大高度和第二高的节点，对于每一层，我们需要记录：
      • 最大高度（max）
      • 第二高的高度（second）
      • 最大高度节点的值（maxNodeVal）

  3. 计算树的高度：

    • 通过递归方式遍历树的每个节点，在遍历过程中计算每个节点的高度，并更新 heightMap 和 levelsMap。

  4. 处理查询：

    • 对于每个查询，首先获取待删除节点的高度和深度。
    • 检查该节点是否为其所在层的最大高度节点：
      • 如果是，新的树高度为 rootHeight - max + second（即去掉最大高度节点的影响，使用第二高的高度）。
      • 如果不是，树的高度保持不变，即 rootHeight。

  5. 返回结果：

    • 将每个查询的结果存储到数组中，并最终返回该数组。

复杂度分析

  • 时间复杂度：O(n + m)，其中 n 为树的节点数，m 为查询的数量；
    • DFS 计算高度和层级信息的时间复杂度为 O(n)；
    • 查询每个节点的高度的时间复杂度为 O(1)，总查询复杂度为 O(m)；
  • 空间复杂度：O(n)，存储每个节点信息的 heightMap 和 levelsMap 的空间复杂度均为 O(n)；

代码

/**
 * @param {TreeNode} root
 * @param {number[]} queries
 * @return {number[]}
 */
var treeQueries = function (root, queries) {
	let heightMap = new Map();
	let levelsMap = new Map();

	// DFS 计算高度并记录每层的最大和第二高
	calculateHeight(root, heightMap, levelsMap, 0);

	const res = [];
	const rootHeight = heightMap.get(root.val)[0];

	for (let num of queries) {
		const [height, deep] = heightMap.get(num);
		const { max, second, maxNodeVal } = levelsMap.get(deep);
		// 检查该节点是否为其所在层的最大高度节点
		if (num === maxNodeVal) {
			res.push(rootHeight - max + second);
		} else {
			res.push(rootHeight);
		}
	}

	return res;
};

var calculateHeight = function (node, heightMap, levelsMap, deep) {
	if (!node) return -1;

	const left = calculateHeight(node.left, heightMap, levelsMap, deep + 1);
	const right = calculateHeight(node.right, heightMap, levelsMap, deep + 1);
	const height = 1 + Math.max(left, right);

	heightMap.set(node.val, [height, deep]);

	if (!levelsMap.has(deep)) {
		levelsMap.set(deep, { max: height, second: -1, maxNodeVal: node.val });
	} else {
		const levelInfo = levelsMap.get(deep);
		if (height > levelInfo.max) {
			levelInfo.second = levelInfo.max;
			levelInfo.max = height;
			levelInfo.maxNodeVal = node.val;
		} else if (height > levelInfo.second) {
			levelInfo.second = height;
		}
	}

	return height;
};

相关题目

题号标题题解标签难度
104二叉树的最大深度open in new window[✓]树 深度优先搜索 广度优先搜索 1+
Copyright © 2024 2xiao