2463. 最小移动总距离

🔴   🔖  数组 动态规划 排序  🔗 力扣 LeetCode

题目

There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment , you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.

Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.

Note that

• All robots move at the same speed.
• If two robots move in the same direction, they will never collide.
• If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
• If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
• If the robot moved from a position x to a position y, the distance it moved is |y - x|.

Example 1:

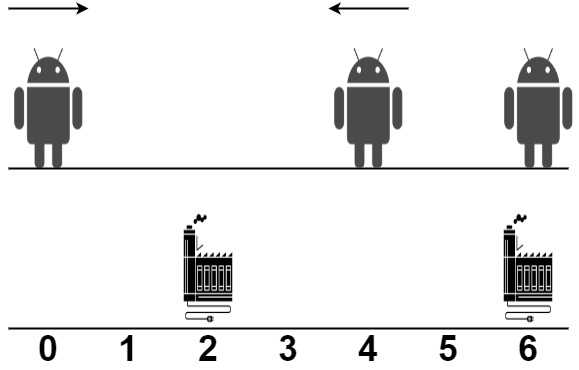
Input: robot = [0,4,6], factory = [[2,2],[6,2]]

Output: 4

Explanation: As shown in the figure:

• The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
• The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
• The third robot at position 6 will be repaired at the second factory. It does not need to move.

The limit of the first factory is 2, and it fixed 2 robots.

The limit of the second factory is 2, and it fixed 1 robot.

The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.

Example 2:

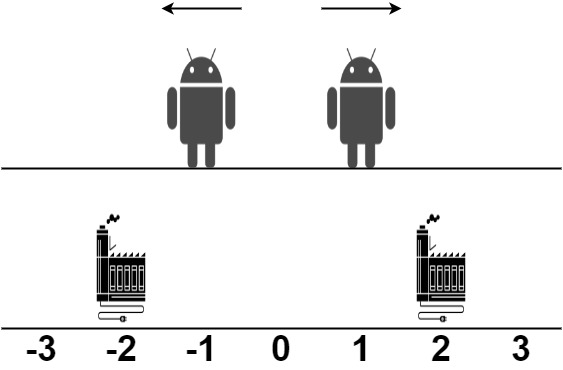
Input: robot = [1,-1], factory = [[-2,1],[2,1]]

Output: 2

Explanation: As shown in the figure:

• The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
• The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.

The limit of the first factory is 1, and it fixed 1 robot.

The limit of the second factory is 1, and it fixed 1 robot.

The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.

Constraints:

• 1 <= robot.length, factory.length <= 100
• factory[j].length == 2
• -10^9 <= robot[i], positionj <= 10^9
• 0 <= limitj <= robot.length
• The input will be generated such that it is always possible to repair every robot.

题目大意

X 轴上有一些机器人和工厂。给你一个整数数组 robot ，其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ，其中 factory[j] = [positionj, limitj] ，表示第 j 个工厂的位置在 positionj ，且第 j 个工厂最多可以修理 limitj 个机器人。

每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。

所有机器人一开始都是坏的，他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向，要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时，这个工厂会维修这个机器人，且机器人停止移动。

任何时刻 ，你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。

请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。

注意：

• 所有机器人移动速度相同。
• 如果两个机器人移动方向相同，它们永远不会碰撞。
• 如果两个机器人迎面相遇，它们也不会碰撞，它们彼此之间会擦肩而过。
• 如果一个机器人经过了一个已经达到上限的工厂，机器人会当作工厂不存在，继续移动。
• 机器人从位置 x 到位置 y 的移动距离为 |y - x| 。

示例 1：

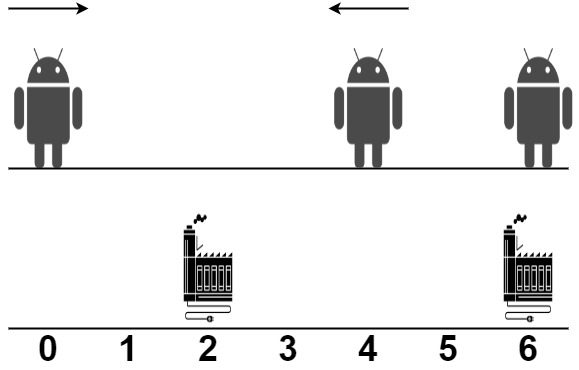
输入： robot = [0,4,6], factory = [[2,2],[6,2]]

输出： 4

解释： 如上图所示：

• 第一个机器人从位置 0 沿着正方向移动，在第一个工厂处维修。
• 第二个机器人从位置 4 沿着负方向移动，在第一个工厂处维修。
• 第三个机器人在位置 6 被第二个工厂维修，它不需要移动。

第一个工厂的维修上限是 2 ，它维修了 2 个机器人。

第二个工厂的维修上限是 2 ，它维修了 1 个机器人。

总移动距离是 |2 - 0| + |2 - 4| + |6 - 6| = 4 。没有办法得到比 4 更少的总移动距离。

示例 2：

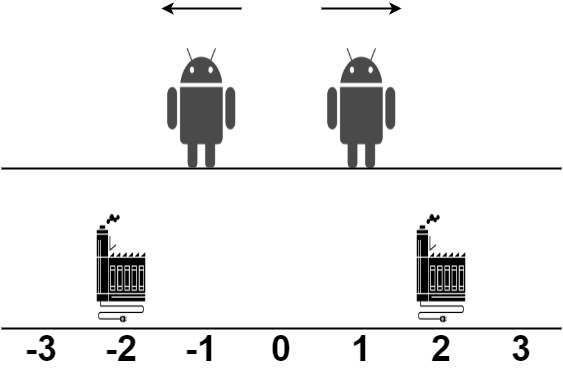
输入： robot = [1,-1], factory = [[-2,1],[2,1]]

输出： 2

解释： 如上图所示：

• 第一个机器人从位置 1 沿着正方向移动，在第二个工厂处维修。
• 第二个机器人在位置 -1 沿着负方向移动，在第一个工厂处维修。

第一个工厂的维修上限是 1 ，它维修了 1 个机器人。

第二个工厂的维修上限是 1 ，它维修了 1 个机器人。

总移动距离是 |2 - 1| + |(-2) - (-1)| = 2 。没有办法得到比 2 更少的总移动距离。

提示：

• 1 <= robot.length, factory.length <= 100
• factory[j].length == 2
• -10^9 <= robot[i], positionj <= 10^9
• 0 <= limitj <= robot.length
• 测试数据保证所有机器人都可以被维修。

解题思路

可以使用动态规划来解决这个问题。

1. 排序：首先对机器人和工厂的位置进行排序，以便于后续的计算。

2. 动态规划表：创建一个二维数组 dp，其中 dp[i][j] 表示前 i 个机器人使用前 j 个工厂的最小移动距离。

3. 初始化：

   • 初始化 dp[0][0] = 0，表示没有机器人和工厂的情况，总移动距离为 0。
   • 对于其他状态，可以初始化为无穷大（表示不可能的状态）。

4. 状态转移：

   • 使用内层循环来尝试当前工厂修理 k 个机器人，k 的范围是从 0 到当前工厂的限制（即 limit[j]），并且不能超过当前机器人的数量 i。

   • 若不使用当前工厂，即：k = 0 时，dp[i][j] = dp[i][j - 1]；

   • 若使用当前工厂修理 1 个机器人，即 k = 1 时，dp[i][j] = dp[i - 1][j - 1] + distance；

     • 其中 distance 是第 i 个机器人到第 j 个工厂的距离，即 distance = Math.abs(robot[i - 1] - factory[j - 1][0])；

   • 依此类推，遍历所有可能的 k 种情况，找出 dp[i][j] 的最小值。

5. 结果返回：返回 dp[n][m]，即所有机器人使用所有工厂的最小总距离。

复杂度分析

• 时间复杂度：O(n * m * limit)，其中 n 是机器人的数量，m 是工厂的数量，limit 是所有工厂的最大修理能力。
• 空间复杂度：O(n * m)，用于存储 dp 表。

代码

/**
 * @param {number[]} robot
 * @param {number[][]} factory
 * @return {number}
 */
var minimumTotalDistance = function (robot, factory) {
	// 将工厂和机器人按位置排序
	robot.sort((a, b) => a - b);
	factory.sort((a, b) => a[0] - b[0]);

	const n = robot.length,
		m = factory.length;

	// dp[i][j] 表示前 i 个机器人用前 j 个工厂的最小总距离
	let dp = new Array(n + 1).fill(0).map((i) => new Array(m + 1).fill(Infinity));

	// 初始状态，0 个机器人和 0 个工厂的总距离为 0
	dp[0][0] = 0;

	for (let j = 1; j <= m; j++) {
		const [position, limit] = factory[j - 1];
		for (let i = 0; i <= n; i++) {
			// 不使用这个工厂的情况
			dp[i][j] = dp[i][j - 1];
			let distance = 0;
			// 尝试用当前工厂修理 k 个机器人
			for (let k = 1; k <= limit && i >= k; k++) {
				distance += Math.abs(robot[i - k] - position);
				dp[i][j] = Math.min(dp[i][j], dp[i - k][j - 1] + distance);
			}
		}
	}

	return dp[n][m];
};

相关题目

题号	标题	题解	标签	难度	力扣
1011	在 D 天内送达包裹的能力		数组 二分查找	🟠	🀄️ 🔗
2585	获得分数的方法数		数组 动态规划	🔴	🀄️ 🔗