2579. 统计染色格子数
2579. 统计染色格子数
题目
There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:
- At the first minute, color any arbitrary unit cell blue.
- Every minute thereafter, color blue every uncolored cell that touches a blue cell.
Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.
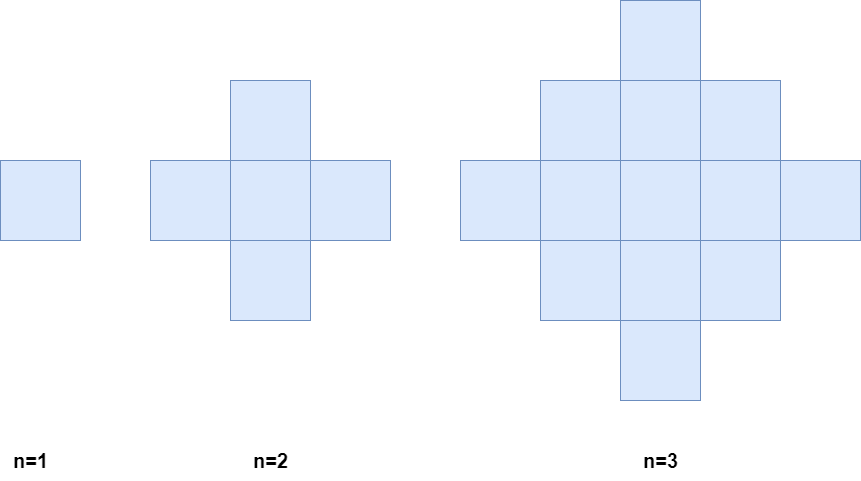
Return _the number ofcolored cells at the end of _n minutes.
Example 1:
Input: n = 1
Output: 1
Explanation: After 1 minute, there is only 1 blue cell, so we return 1.
Example 2:
Input: n = 2
Output: 5
Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.
Constraints:
1 <= n <= 10^5
题目大意
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:
- 第一分钟,将 任一 格子染成蓝色。
- 之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。
下图分别是 1、2、3 分钟后的网格图。

请你返回 n 分钟之后 被染色的格子 数目。
示例 1:
输入: n = 1
输出: 1
解释: 1 分钟后,只有 1 个蓝色的格子,所以返回 1 。
示例 2:
输入: n = 2
输出: 5
解释: 2 分钟后,有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子,所以返回 5 。
提示:
1 <= n <= 10^5
解题思路
题目要求计算 n 层正方形网格 中 被涂色的单元格总数。可以观察到:
- n=1 时,只有 1 个单元格。
- n=2 时,在 n=1 的基础上增加了 4 个单元格。
- n=3 时,在 n=2 的基础上增加了 8 个单元格。
通过归纳可以发现:
- 第
n层的新增单元格数量为4 * (n - 1)。 - 递推公式:
f(n) = f(n - 1) + 4(n - 1) - 初始条件:
f(1) = 1
递归会导致 O(n) 递归深度,可以转换为 数学公式求解:
展开递推公式:
f(n) = 1 + 4 * 1 + 4 * 2 + 4 * 3 + ... + 4(n - 2) + 4(n - 1)提取
4,转换为等差数列求和:f(n) = 1 + 4 * ((n - 1) * n / 2)最终公式:
f(n) = 1 + 2(n - 1) * n时间复杂度:
O(1),直接使用公式计算。空间复杂度:
O(1),没有使用其他参数。
代码
/**
* @param {number} n
* @return {number}
*/
var coloredCells = function (n) {
return 1 + 2 * n * (n - 1);
};
相关题目
| 题号 | 标题 | 题解 | 标签 | 难度 | 力扣 |
|---|---|---|---|---|---|
| 2481 | 分割圆的最少切割次数 | [✓] | 几何 数学 | 🟢 | 🀄️ 🔗 |
