1975. 最大方阵和

🟠   🔖  贪心 数组 矩阵  🔗 力扣 LeetCode

题目

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return themaximum sum of the matrix's elements using the operation mentioned above.

Example 1:

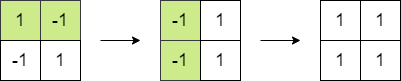
Input: matrix = [[1,-1],[-1,1]]

Output: 4

Explanation: We can follow the following steps to reach sum equals 4:

• Multiply the 2 elements in the first row by -1.
• Multiply the 2 elements in the first column by -1.

Example 2:

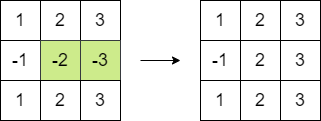
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]

Output: 16

Explanation: We can follow the following step to reach sum equals 16:

• Multiply the 2 last elements in the second row by -1.

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -10^5 <= matrix[i][j] <= 10^5

题目大意

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

• 选择 matrix 中 相邻 两个元素，并将它们都 乘以 -1 。

如果两个元素有 公共边 ，那么它们就是 相邻 的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的 最大 和。

示例 1：

输入： matrix = [[1,-1],[-1,1]]

输出： 4

解释： 我们可以执行以下操作使和等于 4 ：

• 将第一行的 2 个元素乘以 -1 。
• 将第一列的 2 个元素乘以 -1 。

示例 2：

输入： matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]

输出： 16

解释： 我们可以执行以下操作使和等于 16 ：

• 将第二行的最后 2 个元素乘以 -1 。

提示：

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -10^5 <= matrix[i][j] <= 10^5

解题思路

最大化矩阵元素和的关键在于：

• 尽量使负数变为正数。
• 如果某些负数无法翻转符号，我们需要减少它们对总和的影响。

1. 计算矩阵的绝对值总和：
   • 对于所有元素的绝对值相加，假设所有元素都能变为正数，这是理论上的最大可能总和。
2. 统计负数的个数：
   • 如果负数的个数为偶数，通过多次翻转操作可以将所有负数变为正数。
   • 如果负数的个数为奇数，最终会剩下一个负数。
3. 处理奇数个负数的情况：
   • 找到矩阵中绝对值最小的元素（不论正负），如果无法完全消除负数，可以将这个绝对值最小的元素翻转为负，从而对总和影响最小。

复杂度分析

• 时间复杂度：O(n^2)，遍历矩阵所有元素。
• 空间复杂度：O(1)，使用了常数级别的辅助变量。

代码

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var maxMatrixSum = function (matrix) {
	let totalSum = 0; // 矩阵绝对值总和
	let minAbs = Infinity; // 矩阵中绝对值最小的元素
	let negativeCount = 0; // 负数个数

	for (let row of matrix) {
		for (let val of row) {
			totalSum += Math.abs(val); // 统计绝对值总和
			minAbs = Math.min(minAbs, Math.abs(val)); // 更新绝对值最小的值
			if (val < 0) negativeCount++; // 统计负数个数
		}
	}

	// 如果负数个数为偶数，所有负数都能消除
	// 如果负数个数为奇数，剩下的负数会减去最小绝对值的两倍
	return negativeCount % 2 === 0 ? totalSum : totalSum - 2 * minAbs;
};