1971. 寻找图中是否存在路径
1971. 寻找图中是否存在路径
🟢 🔖 深度优先搜索 广度优先搜索 并查集 图 🔗 力扣 LeetCode
题目
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true _if there is avalid path from _source todestination , orfalseotherwise .
Example 1:
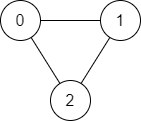
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
Example 2:
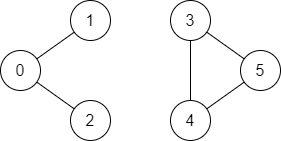
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
1 <= n <= 2 * 10^50 <= edges.length <= 2 * 10^5edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- There are no duplicate edges.
- There are no self edges.
题目大意
有一个具有 n 个顶点的 双向 图,其中每个顶点标记从 0 到 n - 1(包含 0 和 n - 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始,到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false 。
示例 1:

输入: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出: true
解释: 存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2
- 0 → 2
示例 2:

输入: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出: false
解释: 不存在由顶点 0 到顶点 5 的路径.
提示:
1 <= n <= 2 * 10^50 <= edges.length <= 2 * 10^5edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- 不存在重复边
- 不存在指向顶点自身的边
解题思路
特殊情况处理:
- 如果起点
source和终点destination相同,则无需任何计算,直接返回true。
- 如果起点
构建图的邻接表:
- 使用邻接表表示图,方便存储节点之间的连接关系。
- 遍历
edges数组,将每条边的两个节点相互添加到邻接表中,以便于查询相邻节点。
初始化 BFS:
- 使用队列存储当前访问的节点,从起点
source开始。 - 使用一个
visited数组标记访问过的节点,避免重复遍历,降低时间复杂度。
- 使用队列存储当前访问的节点,从起点
执行 BFS:
- 每次从队列中取出一个节点
node,检查它的所有相邻节点:- 如果相邻节点为
destination,直接返回true。 - 如果相邻节点未访问过,标记为已访问,并将其加入队列继续遍历。
- 如果相邻节点为
- 如果队列为空且未找到
destination,则返回false。
- 每次从队列中取出一个节点
结束条件:
- BFS 的终止条件为队列为空或找到目标节点
destination。
- BFS 的终止条件为队列为空或找到目标节点
复杂度分析
时间复杂度:
O(V + E)- 构建图的时间复杂度为
O(E),其中E是边的数量。 - BFS 遍历所有节点和边的时间复杂度为
O(V + E),其中V是节点数量。 - 总体时间复杂度为
O(V + E)。
- 构建图的时间复杂度为
空间复杂度:
O(V + E)- 图的存储空间为
O(V + E)。 - 访问数组和队列的空间为
O(V)。 - 总体空间复杂度为
O(V + E)。
- 图的存储空间为
代码
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} source
* @param {number} destination
* @return {boolean}
*/
var validPath = function (n, edges, source, destination) {
if (source === destination) return true;
// 构建图
let graph = new Array(n).fill().map(() => []);
for (let [a, b] of edges) {
graph[a].push(b);
graph[b].push(a);
}
// BFS 搜索
let queue = [source];
let visited = new Array(n).fill(false);
visited[source] = true;
while (queue.length > 0) {
let node = queue.shift();
for (let neighbor of graph[node]) {
if (neighbor === destination) {
return true;
}
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
}
}
return false;
};
相关题目
| 题号 | 标题 | 题解 | 标签 | 难度 | 力扣 |
|---|---|---|---|---|---|
| 2077 | 殊途同归 🔒 | 图 | 🟠 | 🀄️ 🔗 | |
| 2097 | 合法重新排列数对 | [✓] | 深度优先搜索 图 欧拉回路 | 🔴 | 🀄️ 🔗 |
