1791. 找出星型图的中心节点
1791. 找出星型图的中心节点
题目
There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.
You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.
Example 1:
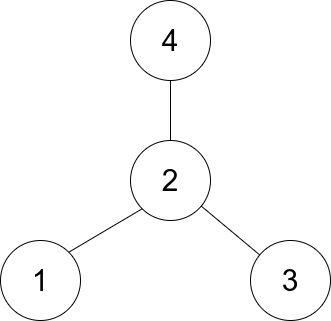
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.
Example 2:
Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1
Constraints:
3 <= n <= 10^5edges.length == n - 1edges[i].length == 21 <= ui, vi <= nui != vi- The given
edgesrepresent a valid star graph.
题目大意
有一个无向的 星型 图,由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点,并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。
给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。
示例 1:

输入: edges = [[1,2],[2,3],[4,2]]
输出: 2
解释: 如上图所示,节点 2 与其他每个节点都相连,所以节点 2 是中心节点。
示例 2:
输入: edges = [[1,2],[5,1],[1,3],[1,4]]
输出: 1
提示:
3 <= n <= 10^5edges.length == n - 1edges[i].length == 21 <= ui, vi <= nui != vi- 题目数据给出的
edges表示一个有效的星型图
解题思路
图的中心节点是连接所有其他节点的节点。因此,中心节点一定是出现在两条边中的共同节点。
根据星型图的性质,任意两个边中,至少有一个端点是重合的,重合的端点就是我们要找的中心节点。
分析输入:
- 任意取两条边,假设取
edges[0]和edges[1],每条边都包含两个节点。 - 边的信息为
[[a1, b1], [a2, b2]],每条边分别连接了节点a1、b1和节点a2、b2。
- 任意取两条边,假设取
判断中心节点:
- 检查
a1和b1是否出现在两条边中。如果a1 == a2或a1 == b2,说明a1是中心节点;否则,b1就是中心节点。
- 检查
复杂度分析
- 时间复杂度:
O(1),只进行了一次简单的比较。 - 空间复杂度:
O(1),只使用了常数空间。
代码
/**
* @param {number[][]} edges
* @return {number}
*/
var findCenter = function (edges) {
const [a1, b1] = edges[0];
const [a2, b2] = edges[1];
if (a1 == a2 || a1 == b2) return a1;
return b1;
};
相关题目
| 题号 | 标题 | 题解 | 标签 | 难度 | 力扣 |
|---|---|---|---|---|---|
| 2497 | 图中最大星和 | 贪心 图 数组 2+ | 🟠 | 🀄️ 🔗 |
