1765. 地图中的最高点
1765. 地图中的最高点
🟠 🔖 广度优先搜索 数组 矩阵 🔗 力扣 LeetCode
题目
You are given an integer matrix isWater of size m x n that represents a map of land and water cells.
- If
isWater[i][j] == 0, cell(i, j)is a land cell. - If
isWater[i][j] == 1, cell(i, j)is a water cell.
You must assign each cell a height in a way that follows these rules:
- The height of each cell must be non-negative.
- If the cell is a water cell, its height must be
0. - Any two adjacent cells must have an absolute height difference of at most
1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is maximized.
Return an integer matrixheight of sizem x n whereheight[i][j]is cell (i, j) ' s height. If there are multiple solutions, return any of them.
Example 1:
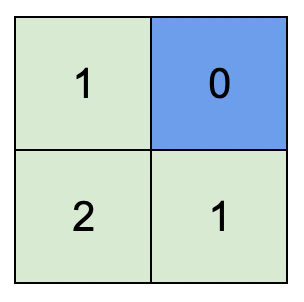
Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
Example 2:
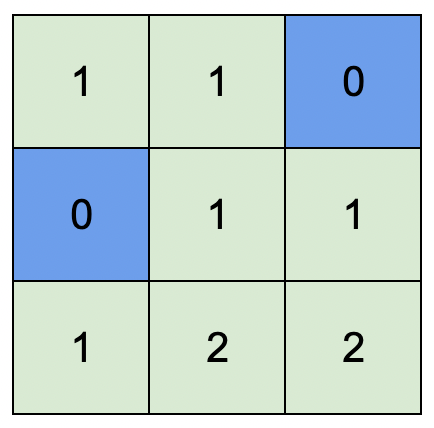
Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output: [[1,1,0],[0,1,1],[1,2,2]]
Explanation: A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
Constraints:
m == isWater.lengthn == isWater[i].length1 <= m, n <= 1000isWater[i][j]is0or1.- There is at least one water cell.
题目大意
给你一个大小为 m x n 的整数矩阵 isWater ,它代表了一个由 陆地 和 水域 单元格组成的地图。
- 如果
isWater[i][j] == 0,格子(i, j)是一个 陆地 格子。 - 如果
isWater[i][j] == 1,格子(i, j)是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度:
- 每个格子的高度都必须是非负的。
- 如果一个格子是 水域 ,那么它的高度必须为
0。 - 任意相邻的格子高度差 至多 为
1。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)
找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ,其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法,请返回 任意一个 。
示例 1:

输入: isWater = [[0,1],[0,0]]
输出:[[1,0],[2,1]]
解释: 上图展示了给各个格子安排的高度。
蓝色格子是水域格,绿色格子是陆地格。
示例 2:

输入: isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出:[[1,1,0],[0,1,1],[1,2,2]]
解释: 所有安排方案中,最高可行高度为 2 。
任意安排方案中,只要最高高度为 2 且符合上述规则的,都为可行方案。
提示:
m == isWater.lengthn == isWater[i].length1 <= m, n <= 1000isWater[i][j]要么是0,要么是1。- 至少有 1 个水域格子。
解题思路
解题思路
可以采用广度优先搜索(BFS)策略,将每个水源格子作为 BFS 的起点,逐步向外扩展,更新每个格子的高度为其与水源的距离,同时结合 Deque 来优化性能。
- 初始化:
- 创建结果数组
res,初始值为-1,表示尚未访问的格子。 - 将所有水源格子(值为
1)入队,初始高度设为0。
- 创建结果数组
- 双端队列:
- 使用双端队列(Deque)来代替原生数组模拟队列。
- 队首指针 (
head): 用于取出元素,完成shift操作。 - 队尾指针 (
tail): 用于插入元素,完成push操作。 - 性能优势: 原生数组的
shift是O(n),在高频操作下显著拖累性能。使用Deque实现的队列,push和shift均为O(1)。
- 广度优先搜索:
- 每次从队首取出一个格子,尝试向四个方向扩展。
- 对于未访问过的格子(
res值为-1),将其高度设为当前高度 + 1,并加入队列。
- 终止条件:
- 队列为空时,所有格子均已访问,搜索结束。
- 返回结果:
- 输出构建好的结果数组。
复杂度分析
- 时间复杂度:
O(m * n),BFS 遍历每个格子一次。 - 空间复杂度:
O(m * n),结果数组和队列占用的存储空间。
代码
/**
* @param {number[][]} isWater
* @return {number[][]}
*/
var highestPeak = function (isWater) {
const m = isWater.length;
const n = isWater[0].length;
const res = Array.from({ length: m }, () => Array(n).fill(-1));
const queue = new MyDeque();
// 初始化水源点
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (isWater[i][j] === 1) {
queue.push([i, j]); // 双端队列尾部插入
res[i][j] = 0;
}
}
}
const directions = [
[1, 0],
[-1, 0],
[0, 1],
[0, -1]
];
// 广度优先搜索
while (!queue.isEmpty()) {
const [x, y] = queue.shift(); // 双端队列头部取出
for (const [dx, dy] of directions) {
const nx = x + dx;
const ny = y + dy;
// 检查边界并判断是否已访问
if (nx >= 0 && nx < m && ny >= 0 && ny < n && res[nx][ny] === -1) {
res[nx][ny] = res[x][y] + 1;
queue.push([nx, ny]); // 双端队列尾部插入
}
}
}
return res;
};
// 定义简单的双端队列类
class MyDeque {
constructor() {
this.data = [];
this.head = 0; // 队首指针
this.tail = 0; // 队尾指针
}
push(value) {
this.data[this.tail++] = value; // 插入队尾
}
shift() {
if (this.isEmpty()) return null;
const value = this.data[this.head];
this.head++;
return value; // 取出队首
}
isEmpty() {
return this.head === this.tail;
}
}
